После сбора соответствующих данных, мы должны проанализировать их соответствующим образом. Есть три основных момента, которые следует учитывать при выборе метода анализа.
- Природа данных
- Цель эксперимента
- Особенности дизайна
Природа данных
Чтобы проанализировать данные, мы также должны посмотреть на большую популяцию, представленную данными, а также на распределение этих данных.
Выборка, население и распределение данных
Выборка — это процесс выбора набора данных из большой совокупности. Выборочная статистика описывает и обобщает показатели, полученные от группы экспериментальных субъектов.
Параметры популяции представляют собой значения, которые были бы получены, если бы были измерены все возможные предметы.
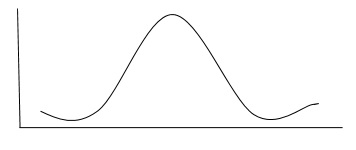
Популяцию или выборку можно описать показателями центральной тенденции, такими как среднее значение, медиана и способ, и показателями дисперсии, такими как дисперсия и стандартное отклонение. Многие наборы данных распределяются нормально, как показано на следующем графике.
Как показано выше, данные будут равномерно распределены по среднему значению. что является существенными характеристиками нормального распределения.
Другие распределения также существуют, когда данные искажены, так что на одной стороне от среднего значения больше точек данных, чем на другой. Например: если большая часть данных присутствует в левой части среднего значения, то можно сказать, что распределение искажено влево.
Цель эксперимента
Обычно проводятся эксперименты —
- Чтобы подтвердить теорию
- Чтобы исследовать отношения
Для достижения каждого из них, цель должна быть формально выражена в терминах гипотезы, а анализ должен непосредственно касаться гипотезы.
Чтобы подтвердить теорию
Расследование должно быть направлено на изучение истинности теории. Теория обычно утверждает, что использование определенного метода, инструмента или техники оказывает особый эффект на субъектов, делая его лучше тем или иным способом.
Необходимо рассмотреть два случая данных: нормальные данные и ненормальные данные .
Если данные взяты из нормального распределения и есть две группы для сравнения, для анализа можно использовать t-критерий Стьюдента. Если нужно сравнить более двух групп, можно использовать общий анализ дисперсии, называемый F-статистикой.
Если данные не являются нормальными, то данные могут быть проанализированы с помощью теста Крускала-Уоллиса путем ранжирования.
Чтобы исследовать отношения
Исследования предназначены для определения взаимосвязи между точками данных, описывающими одну переменную или несколько переменных.
Есть три метода, чтобы ответить на вопросы об отношениях: коробочные графики, точечные диаграммы и корреляционный анализ.
-
Квадратный график может представлять сводку диапазона набора данных.
-
Диаграмма разброса представляет связь между двумя переменными.
-
Корреляционный анализ использует статистические методы, чтобы подтвердить, существует ли истинная связь между двумя атрибутами.
-
Для нормально распределенных значений используйте коэффициент корреляции Пирсона, чтобы проверить, сильно ли коррелируют две переменные.
-
Для ненормальных данных ранжируйте данные и используйте коэффициент корреляции ранга Спирмена в качестве меры ассоциации. Другой мерой для ненормальных данных является надежный коэффициент корреляции Кендалла , который исследует взаимосвязь между парами точек данных и может идентифицировать частичную корреляцию.
-
Квадратный график может представлять сводку диапазона набора данных.
Диаграмма разброса представляет связь между двумя переменными.
Корреляционный анализ использует статистические методы, чтобы подтвердить, существует ли истинная связь между двумя атрибутами.
Для нормально распределенных значений используйте коэффициент корреляции Пирсона, чтобы проверить, сильно ли коррелируют две переменные.
Для ненормальных данных ранжируйте данные и используйте коэффициент корреляции ранга Спирмена в качестве меры ассоциации. Другой мерой для ненормальных данных является надежный коэффициент корреляции Кендалла , который исследует взаимосвязь между парами точек данных и может идентифицировать частичную корреляцию.
Если ранжирование содержит большое количество связанных значений, можно использовать критерий хи-квадрат для таблицы сопряженности для проверки связи между переменными. Аналогично, линейная регрессия может быть использована для генерации уравнения для описания взаимосвязи между переменными.
Для более чем двух переменных можно использовать многомерную регрессию .
Особенности дизайна
План исследования должен учитываться при выборе методов анализа. В то же время, сложность анализа может влиять на выбранный дизайн. Несколько групп используют F-статистику, а не T-критерий Стьюдента с двумя группами.
Для сложных факторных планов с более чем двумя факторами необходим более сложный тест связи и значимости.
Статистические методы могут использоваться для учета влияния одного набора переменных на другие или для компенсации временных или учебных эффектов.