СУБД — нормализация

Функциональная зависимость (FD) — это набор ограничений между двумя атрибутами в отношении. Функциональная зависимость говорит, что если два кортежа имеют одинаковые значения для атрибутов A1, A2, …, An, то эти два кортежа должны иметь одинаковые значения для атрибутов B1, B2, …, Bn.

Функциональная зависимость представлена ​​знаком стрелки (→), то есть X → Y, где X функционально определяет Y. Атрибуты левой стороны определяют значения атрибутов с правой стороны.

Аксиомы Армстронга

Если F представляет собой набор функциональных зависимостей, то замыкание F, обозначаемое как F ⁺ , представляет собой набор всех функциональных зависимостей, логически подразумеваемых F. Аксиомы Армстронга представляют собой набор правил, которые при многократном применении генерируют замыкание функциональных зависимостей. ,

• Правило рефлексии — если альфа является набором атрибутов и бета-версией is_subset_of альфа, то альфа содержит бета-версию.

• Правило аугментации — если a → b выполнено, а y является установленным атрибутом, то также выполняется ay → by. То есть добавление атрибутов в зависимости не меняет основных зависимостей.

• Правило транзитивности — То же самое, что и транзитивное правило в алгебре, если выполняется a → b и b → c, то также выполняется a → c. a → b называется функционально определяющим b.

Правило рефлексии — если альфа является набором атрибутов и бета-версией is_subset_of альфа, то альфа содержит бета-версию.

Правило аугментации — если a → b выполнено, а y является установленным атрибутом, то также выполняется ay → by. То есть добавление атрибутов в зависимости не меняет основных зависимостей.

Правило транзитивности — То же самое, что и транзитивное правило в алгебре, если выполняется a → b и b → c, то также выполняется a → c. a → b называется функционально определяющим b.

Тривиальная функциональная зависимость

• Trivial — если выполняется функциональная зависимость (FD) X → Y, где Y — подмножество X, то она называется тривиальной FD. Тривиальные ФД всегда держатся.

• Нетривиальный. Если выполняется FD X → Y, где Y не является подмножеством X, то он называется нетривиальным FD.

• Полностью нетривиальный — если выполняется FD X → Y, где x пересекается с Y = Φ, он называется совершенно нетривиальным FD.

Trivial — если выполняется функциональная зависимость (FD) X → Y, где Y — подмножество X, то она называется тривиальной FD. Тривиальные ФД всегда держатся.

Нетривиальный. Если выполняется FD X → Y, где Y не является подмножеством X, то он называется нетривиальным FD.

Полностью нетривиальный — если выполняется FD X → Y, где x пересекается с Y = Φ, он называется совершенно нетривиальным FD.

нормализация

Если дизайн базы данных не идеален, он может содержать аномалии, которые кажутся плохим сном для любого администратора базы данных. Управление базой данных с аномалиями практически невозможно.

• Обновление аномалий — если элементы данных разбросаны и не связаны должным образом друг с другом, это может привести к странным ситуациям. Например, когда мы пытаемся обновить один элемент данных, копии которого разбросаны по нескольким местам, несколько экземпляров обновляются должным образом, а несколько других остаются со старыми значениями. Такие экземпляры оставляют базу данных в несогласованном состоянии.

• Аномалии удаления — мы пытались удалить запись, но ее части остались неосознанными из-за неосведомленности, данные также сохраняются в другом месте.

• Вставить аномалии — мы попытались вставить данные в запись, которая вообще не существует.

Обновление аномалий — если элементы данных разбросаны и не связаны должным образом друг с другом, это может привести к странным ситуациям. Например, когда мы пытаемся обновить один элемент данных, копии которого разбросаны по нескольким местам, несколько экземпляров обновляются должным образом, а несколько других остаются со старыми значениями. Такие экземпляры оставляют базу данных в несогласованном состоянии.

Аномалии удаления — мы пытались удалить запись, но ее части остались неосознанными из-за неосведомленности, данные также сохраняются в другом месте.

Вставить аномалии — мы попытались вставить данные в запись, которая вообще не существует.

Нормализация — это метод устранения всех этих аномалий и приведения базы данных в согласованное состояние.

Первая нормальная форма

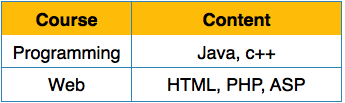
Первая нормальная форма определяется в определении самих отношений (таблиц). Это правило определяет, что все атрибуты в отношении должны иметь атомарные домены. Значения в атомной области являются неделимыми единицами.

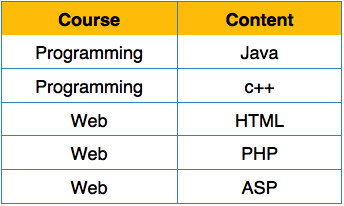
Мы переупорядочиваем отношение (таблицу), как показано ниже, чтобы преобразовать его в первую нормальную форму.

Каждый атрибут должен содержать только одно значение из своего предварительно определенного домена.

Вторая нормальная форма

Прежде чем мы узнаем о второй нормальной форме, мы должны понять следующее —

• Основной атрибут . Атрибут, являющийся частью ключа-кандидата, называется основным атрибутом.

• Непростой атрибут . Атрибут, который не является частью простого ключа, называется непростым атрибутом.

Основной атрибут . Атрибут, являющийся частью ключа-кандидата, называется основным атрибутом.

Непростой атрибут . Атрибут, который не является частью простого ключа, называется непростым атрибутом.

Если мы следуем второй нормальной форме, то каждый непростой атрибут должен полностью функционально зависеть от атрибута первичного ключа. То есть, если X → A выполнено, то не должно быть никакого собственного подмножества Y в X, для которого Y → A также верно.

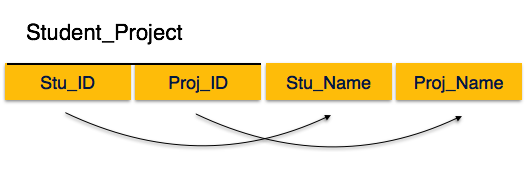
Здесь мы видим в отношении Student_Project, что атрибутами простого ключа являются Stu_ID и Proj_ID. В соответствии с правилом неключевые атрибуты, то есть Stu_Name и Proj_Name, должны зависеть от обоих, а не от какого-либо отдельного атрибута первичного ключа. Но мы обнаруживаем, что Stu_Name может быть идентифицировано Stu_ID, а Proj_Name может быть идентифицировано Proj_ID независимо. Это называется частичной зависимостью , которая не допускается во второй нормальной форме.

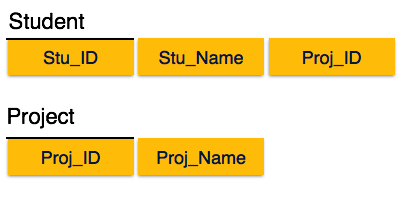
Мы разорвали отношения на две части, как показано на картинке выше. Таким образом, не существует частичной зависимости.

Третья нормальная форма

Чтобы отношение было в третьей нормальной форме, оно должно быть во второй нормальной форме, а следующее должно удовлетворять:

• Ни один не простой атрибут не является транзитивно зависимым от атрибута простого ключа.
• Для любой нетривиальной функциональной зависимости X → A, тогда либо —
  Х это суперключ или,
  • А является основным атрибутом.

Мы обнаруживаем, что в приведенном выше отношении Student_detail Stu_ID является ключевым и единственным атрибутом простого ключа. Мы находим, что Город может быть идентифицирован как Stu_ID, так и самим Zip. Ни Zip не является суперключем, ни City не является главным атрибутом. Кроме того, Stu_ID → Zip → City, поэтому существует транзитивная зависимость .

Чтобы привести это отношение в третью нормальную форму, мы разбиваем отношение на два отношения следующим образом:

Бойс-Кодд Нормальная форма

Нормальная форма Бойса-Кодда (BCNF) является продолжением третьей нормальной формы на строгих условиях. BCNF заявляет, что —

• Для любой нетривиальной функциональной зависимости X → A, X должен быть суперключом.

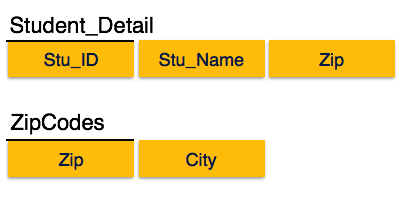
На изображении выше Stu_ID — это супер-ключ в отношении Student_Detail, а Zip — это супер-ключ в отношении ZipCodes. Так,

Stu_ID → Stu_Name, Zip

а также

Zip → Город

Что подтверждает, что оба отношения находятся в BCNF.