Мы знаем, что данные хранятся в виде записей. Каждая запись имеет ключевое поле, которое помогает ее узнавать однозначно.
Индексирование — это метод структуры данных, позволяющий эффективно извлекать записи из файлов базы данных на основе некоторых атрибутов, по которым была выполнена индексация. Индексирование в системах баз данных похоже на то, что мы видим в книгах.
Индексирование определяется на основе его атрибутов индексации. Индексирование может быть следующих типов —
-
Первичный индекс — первичный индекс определяется в упорядоченном файле данных. Файл данных упорядочен по ключевому полю . Поле ключа, как правило, является первичным ключом отношения.
-
Вторичный индекс — Вторичный индекс может быть создан из поля, которое является ключом-кандидатом и имеет уникальное значение в каждой записи, или неключевой ключ с дублирующимися значениями.
-
Индекс кластеризации. Индекс кластеризации определяется в упорядоченном файле данных. Файл данных упорядочен в неключевом поле.
Первичный индекс — первичный индекс определяется в упорядоченном файле данных. Файл данных упорядочен по ключевому полю . Поле ключа, как правило, является первичным ключом отношения.
Вторичный индекс — Вторичный индекс может быть создан из поля, которое является ключом-кандидатом и имеет уникальное значение в каждой записи, или неключевой ключ с дублирующимися значениями.
Индекс кластеризации. Индекс кластеризации определяется в упорядоченном файле данных. Файл данных упорядочен в неключевом поле.
Упорядоченное индексирование бывает двух типов:
- Плотный индекс
- Разреженный индекс
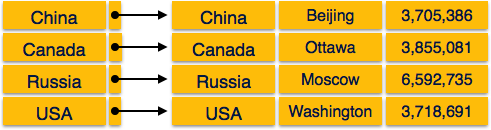
Плотный индекс
В плотном индексе есть индексная запись для каждого значения ключа поиска в базе данных. Это ускоряет поиск, но требует больше места для хранения записей индекса. Индексные записи содержат значение ключа поиска и указатель на фактическую запись на диске.
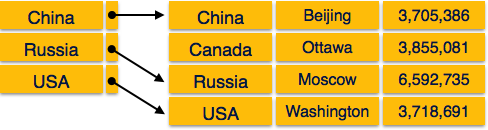
Разреженный индекс
В разреженном индексе записи индекса создаются не для каждого ключа поиска. Индексная запись здесь содержит ключ поиска и фактический указатель на данные на диске. Для поиска записи мы сначала переходим к индексной записи и достигаем фактическое местоположение данных. Если данные, которые мы ищем, находятся не там, где мы непосредственно достигаем, следуя индексу, то система начинает последовательный поиск, пока не будут найдены нужные данные.
Многоуровневый индекс
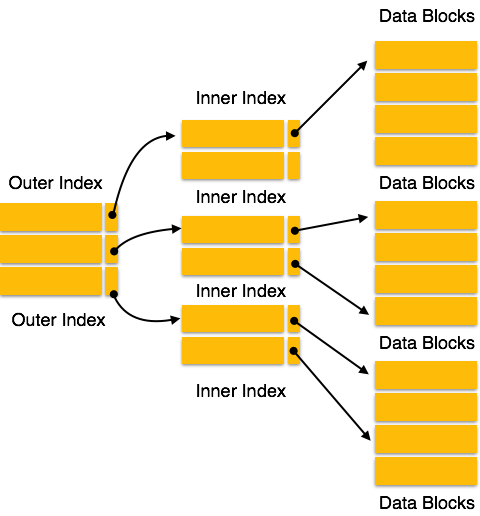
Индексные записи содержат значения ключей поиска и указатели данных. Многоуровневый индекс хранится на диске вместе с актуальными файлами базы данных. По мере увеличения размера базы данных увеличивается и размер индексов. Существует огромная необходимость хранить записи индекса в основной памяти, чтобы ускорить операции поиска. Если используется одноуровневый индекс, индекс большого размера не может быть сохранен в памяти, что приводит к нескольким обращениям к диску.
Многоуровневый индекс помогает разбить индекс на несколько меньших индексов, чтобы сделать внешний уровень настолько маленьким, чтобы его можно было сохранить в одном блоке диска, который можно легко разместить в любом месте основной памяти.
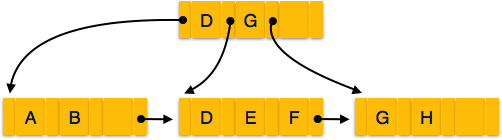
B + Дерево
AB + дерево — это сбалансированное двоичное дерево поиска, которое соответствует многоуровневому формату индекса. Листовые узлы дерева B + обозначают фактические указатели данных. B + дерево гарантирует, что все листовые узлы остаются на одной высоте, таким образом, сбалансированы. Кроме того, конечные узлы связаны с использованием списка ссылок; следовательно, дерево B + может поддерживать произвольный доступ, а также последовательный доступ.
Структура дерева B +
Каждый листовой узел находится на одинаковом расстоянии от корневого узла. Дерево AB + имеет порядок n, где n фиксировано для каждого дерева B + .
Внутренние узлы —
- Внутренние (неконечные) узлы содержат как минимум ⌈n / 2⌉ указателей, кроме корневого узла.
- Максимум, внутренний узел может содержать n указателей.
Листовые узлы —
B + деревья заполняются снизу, и каждая запись выполняется на листовом узле.
Разделите узел на две части.
Разбиение при i = ⌊ (m + 1) / 2 ⌋.
Сначала i записи хранятся в одном узле.
Остальные записи (i + 1 и далее) перемещаются в новый узел.
i- й ключ продублирован у родителя листа.
Если неконечный узел переполняется —
Разделите узел на две части.
Разбейте узел на i = ⌈ (m + 1) / 2 ⌉ .
Записи до i хранятся в одном узле.
Остальные записи перемещаются на новый узел.
Записи дерева B + удаляются в конечных узлах.
Целевая запись ищется и удаляется.
Если это внутренний узел, удалите и замените запись с левой позиции.
После удаления проверяется недостаточное количество
Если происходит переполнение, распределите записи от оставленных ему узлов.
Если распределение слева невозможно, то
Распределите от узлов прямо к нему.
Если распределение не возможно слева или справа, то
Объедините узел с левой и правой стороны.