Схемные соединения в резисторах

Резистор при подключении в цепи, это соединение может быть последовательным или параллельным. Давайте теперь узнаем, что произойдет с суммарными значениями тока, напряжения и сопротивления, если они будут соединены последовательно, а также при параллельном соединении.

Резисторы в серии

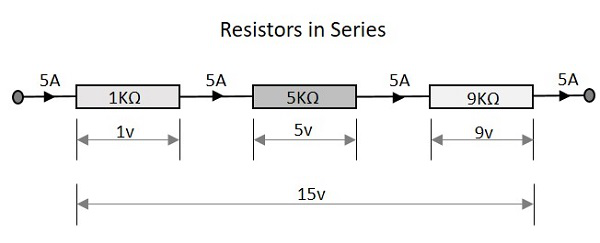
Давайте посмотрим, что происходит, когда несколько последовательно соединенных резисторов. Рассмотрим три резистора с разными значениями, как показано на рисунке ниже.

сопротивление

Общее сопротивление цепи, имеющей последовательные резисторы, равно сумме отдельных сопротивлений. Это означает, что на приведенном выше рисунке три резистора имеют значения 1 кОм, 5 кОм и 9 кОм соответственно.

Общее значение сопротивления резисторной сети составляет —

R=R1 +R2 +R3 $$R \: \: = \: \: R_ {1} \ + \: R_ {2} \ + \: R_ {3}$$

Это означает, что 1 + 5 + 9 = 15 кОм — это полное сопротивление.

Где R ₁ — это сопротивление 1- ^го резистора, R ₂ — это сопротивление 2- ^го резистора, а R ₃ — это сопротивление 3- ^го резистора в вышеуказанной сети резисторов.

вольтаж

Общее напряжение, которое появляется в сети последовательных резисторов, является суммой падений напряжения на каждом отдельном сопротивлении. На рисунке выше у нас есть три разных резистора, которые имеют три разных значения падения напряжения на каждой ступени.

Общее напряжение, которое появляется на цепи —

V=V1 +V2 +V3 $$V \: \: = \: \: V_ {1} \ + \: V_ {2} \ + \: V_ {3}$$

Это означает, что полное напряжение равно 1v + 5v + 9v = 15v.

Где V ₁ — падение напряжения 1- ^го резистора, V ₂ — падение напряжения 2- ^го резистора, а V ₃ — падение напряжения 3- ^го резистора в вышеуказанной сети резисторов.

Текущий

Общее количество тока, протекающего через набор последовательно включенных резисторов, одинаково во всех точках сети резисторов. Следовательно, ток равен 5А при измерении на входе или в любой точке между резисторами или даже на выходе.

Ток через сеть —

I=I1=I2=I3 $$I \: \: = \: \: I_ {1} \: = \: I_ {2} \: = \: I_ {3}$$

Это означает, что ток во всех точках составляет 5А.

Где I ₁ — ток через 1- ^й резистор, I ₂ — ток через 2- ^й резистор, а I ₃ — ток через 3- ^й резистор в вышеупомянутой сети резисторов.

Резисторы параллельно

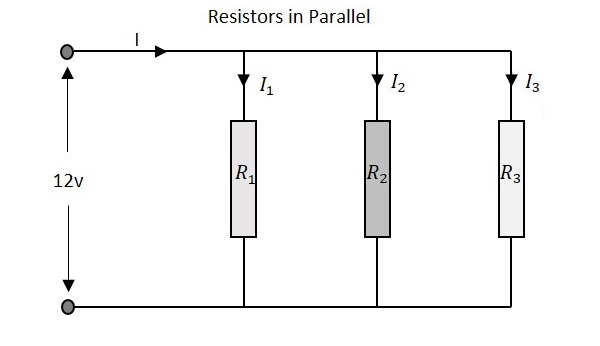
Давайте посмотрим, что происходит, когда несколько резисторов подключены параллельно. Рассмотрим три резистора с разными значениями, как показано на рисунке ниже.

сопротивление

Общее сопротивление цепи, имеющей параллельные резисторы, рассчитывается иначе, чем метод последовательных резисторных сетей. Здесь обратное (1 / R) значение отдельных сопротивлений складывается с обратной величиной алгебраической суммы, чтобы получить общее значение сопротивления.

Общее значение сопротивления резисторной сети составляет —

 гидроразрыва1R,= гидроразрыва1R1 + гидроразрыва1R2 + гидроразрыва1R3 $$\ гидроразрыва {1} {R}, \: \: = \: \: \ гидроразрыва {1} {R_ {1}} \: \ + \: \: \ гидроразрыва {1} {R_ {2}} \: \ + \ гидроразрыва {1} {R_ {3}}$$

Где R ₁ — это сопротивление 1- ^го резистора, R ₂ — это сопротивление 2- ^го резистора, а R ₃ — это сопротивление 3- ^го резистора в вышеуказанной сети резисторов.

Например, если рассматриваются значения сопротивления из предыдущего примера, это означает, что R ₁ = ₁ кОм, R ₂ = 5 кОм и R ₃ = 9 кОм. Общее сопротивление параллельной резисторной сети составит —

 гидроразрыва1R,= гидроразрыва11 + гидроразрыва15 + гидроразрыва19 $$\ гидроразрыва {1} {R}, \: \: = \: \: \ гидроразрыва {1} {1} \: \ + \: \: \ гидроразрыва {1} {5} \: \ + \ гидроразрыва {1} {9}$$

= гидроразрыва45 +9 +545= гидроразрыва5945 $$= \: \: \ гидроразрыва {45 \: \ + \: \: 9 \: \ + \: \: 5} {45} \: \: = \: \: \ гидроразрыва {59} { 45}$$

R= гидроразрыва4559=0.762K Omega=76,2 Omega $$R \: \: = \: \: \ гидроразрыва {45} {59} \: \: = \: \: 0.762K \ Omega \: \: = \: \: 76,2 \ Omega$$

Из метода расчета параллельного сопротивления мы можем вывести простое уравнение для двухрезисторной параллельной сети. Это —

R= гидроразрываR1 разR2R1 +R2  $$R \: \: = \: \: \ гидроразрыва {R_ {1} \: \: \ раз \: \: R_ {2}} {R_ {1} \: \ + \: \: R_ { 2}} \ $$

вольтаж

Общее напряжение, которое появляется в сети параллельных резисторов, совпадает с падением напряжения на каждом отдельном сопротивлении.

Напряжение, которое появляется на цепи —

V=V1=V2=V3 $$V \: \: = \: \: V_ {1} \: = \: V_ {2} \: = \: V_ {3}$$

Где V ₁ — падение напряжения 1- ^го резистора, V ₂ — падение напряжения 2- ^го резистора, а V ₃ — падение напряжения 3- ^го резистора в вышеуказанной сети резисторов. Следовательно, напряжение одинаково во всех точках параллельной сети резисторов.

Текущий

Общее количество тока, поступающего в параллельную резистивную сеть, представляет собой сумму всех отдельных токов, протекающих во всех параллельных ветвях. Значение сопротивления каждой ветви определяет значение тока, протекающего через нее. Общий ток через сеть

I=I1 +I2 +I3 $$I \: \: = \: \: I_ {1} \ + \: I_ {2} \ + \: I_ {3}$$

Где I ₁ — ток через 1- ^й резистор, I ₂ — ток через 2- ^й резистор, а I ₃ — ток через 3- ^й резистор в вышеупомянутой сети резисторов. Следовательно, сумма отдельных токов в разных ветвях позволяет получить суммарный ток в параллельной резистивной сети.

Резистор особенно используется в качестве нагрузки на выходе многих цепей. Если резистивная нагрузка вообще не используется, перед нагрузкой устанавливается резистор. Резистор обычно является основным компонентом в любой цепи.