Шифрование с открытым ключом

В отличие от криптографии с симметричным ключом, мы не находим исторического использования криптографии с открытым ключом. Это относительно новая концепция.

Симметричная криптография хорошо подходила для таких организаций, как правительства, военные и крупные финансовые корпорации, которые были вовлечены в секретную коммуникацию.

С распространением в последние несколько десятилетий более незащищенных компьютерных сетей возникла реальная потребность в использовании криптографии в более широком масштабе. Симметричный ключ оказался непрактичным из-за проблем, с которыми он столкнулся при управлении ключами. Это дало начало криптосистемам с открытым ключом.

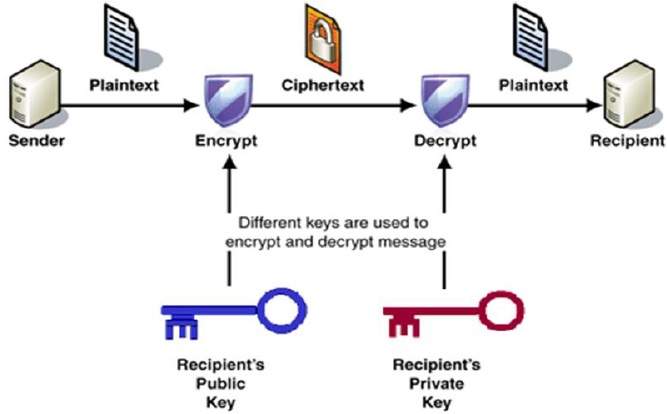
Процесс шифрования и дешифрования изображен на следующей иллюстрации —

Наиболее важные свойства схемы шифрования с открытым ключом —

• Различные ключи используются для шифрования и дешифрования. Это свойство, которое устанавливает эту схему отличной от симметричной схемы шифрования.

• Каждый получатель обладает уникальным ключом дешифрования, обычно называемым его личным ключом.

• Получатель должен опубликовать ключ шифрования, называемый его открытым ключом.

• В этой схеме требуется некоторая гарантия подлинности открытого ключа, чтобы избежать подмены противником в качестве получателя. Как правило, в этом типе криптосистемы задействована доверенная третья сторона, которая удостоверяет, что определенный открытый ключ принадлежит только конкретному человеку или объекту.

• Алгоритм шифрования является достаточно сложным, чтобы запретить злоумышленнику выводить открытый текст из зашифрованного текста и ключа шифрования (открытого).

• Хотя закрытый и открытый ключи связаны математически, вычислить закрытый ключ из открытого ключа не представляется возможным. Фактически, интеллектуальная часть любой криптосистемы с открытым ключом заключается в разработке отношений между двумя ключами.

Различные ключи используются для шифрования и дешифрования. Это свойство, которое устанавливает эту схему отличной от симметричной схемы шифрования.

Каждый получатель обладает уникальным ключом дешифрования, обычно называемым его личным ключом.

Получатель должен опубликовать ключ шифрования, называемый его открытым ключом.

В этой схеме требуется некоторая гарантия подлинности открытого ключа, чтобы избежать подмены противником в качестве получателя. Как правило, в этом типе криптосистемы задействована доверенная третья сторона, которая удостоверяет, что определенный открытый ключ принадлежит только конкретному человеку или объекту.

Алгоритм шифрования является достаточно сложным, чтобы запретить злоумышленнику выводить открытый текст из зашифрованного текста и ключа шифрования (открытого).

Хотя закрытый и открытый ключи связаны математически, вычислить закрытый ключ из открытого ключа не представляется возможным. Фактически, интеллектуальная часть любой криптосистемы с открытым ключом заключается в разработке отношений между двумя ключами.

Существует три типа схем шифрования с открытым ключом. Мы обсудим их в следующих разделах —

Криптосистема RSA

Эта криптосистема является одной из исходных систем. Это остается наиболее используемой криптосистемой даже сегодня. Система была изобретена тремя учеными Роном Ривестом, Ади Шамиром и Леном Адлеманом, и, следовательно, она называется криптосистемой RSA.

Мы увидим два аспекта криптосистемы RSA: во-первых, создание пары ключей и, во-вторых, алгоритмы шифрования-дешифрования.

Генерация пары ключей RSA

Каждый человек или сторона, которая желает участвовать в общении с использованием шифрования, должна сгенерировать пару ключей, а именно открытый ключ и закрытый ключ. Процесс генерации ключей описан ниже —

• Генерация модуля RSA (n)

  • Выберите два больших простых числа, p и q.

  • Рассчитайте n = p * q. Для надежного неразрушимого шифрования пусть n будет большим числом, обычно не менее 512 бит.

• Найти производное число (е)

  • Число e должно быть больше 1 и меньше (p — 1) (q — 1).

  • Не должно быть общего множителя для e и (p — 1) (q — 1), за исключением 1. Другими словами, два числа e и (p — 1) (q — 1) взаимно просты.

• Форма открытого ключа

  • Пара чисел (n, e) образует открытый ключ RSA и становится открытой.

  • Интересно, что хотя n является частью открытого ключа, сложность факторизации большого простого числа гарантирует, что злоумышленник не сможет найти за конечное время два простых числа (p & q), использованных для получения n. Это сила ОГА.

• Генерация закрытого ключа

  • Закрытый ключ d рассчитывается из p, q и e. Для данных n и e существует уникальное число d.

  • Число d является обратной величиной e по модулю (p — 1) (q — 1). Это означает, что d является числом, меньшим (p — 1) (q — 1), так что при умножении на e оно равно 1 по модулю (p — 1) (q — 1).

  • Это соотношение записано математически следующим образом:

Генерация модуля RSA (n)

Выберите два больших простых числа, p и q.

Рассчитайте n = p * q. Для надежного неразрушимого шифрования пусть n будет большим числом, обычно не менее 512 бит.

Найти производное число (е)

Число e должно быть больше 1 и меньше (p — 1) (q — 1).

Не должно быть общего множителя для e и (p — 1) (q — 1), за исключением 1. Другими словами, два числа e и (p — 1) (q — 1) взаимно просты.

Форма открытого ключа

Пара чисел (n, e) образует открытый ключ RSA и становится открытой.

Интересно, что хотя n является частью открытого ключа, сложность факторизации большого простого числа гарантирует, что злоумышленник не сможет найти за конечное время два простых числа (p & q), использованных для получения n. Это сила ОГА.

Генерация закрытого ключа

Закрытый ключ d рассчитывается из p, q и e. Для данных n и e существует уникальное число d.

Число d является обратной величиной e по модулю (p — 1) (q — 1). Это означает, что d является числом, меньшим (p — 1) (q — 1), так что при умножении на e оно равно 1 по модулю (p — 1) (q — 1).

Это соотношение записано математически следующим образом:

ed = 1 mod (p − 1)(q − 1)

Расширенный Евклидов Алгоритм принимает p, q и e в качестве входных данных и дает d в качестве выходных данных.

пример

Пример генерации пары ключей RSA приведен ниже. (Для простоты понимания простые числа p & q, взятые здесь, являются небольшими значениями. На практике эти значения очень высоки).

• Пусть два простых числа p = 7 и q = 13. Таким образом, модуль n = pq = 7 x 13 = 91.

• Выберите e = 5, что является допустимым выбором, поскольку не существует числа с общим множителем 5 и (p — 1) (q — 1) = 6 × 12 = 72, кроме 1.

• Пара чисел (n, e) = (91, 5) образует открытый ключ и может быть доступна любому, кому мы хотим отправлять нам зашифрованные сообщения.

• Введите p = 7, q = 13 и e = 5 в расширенный евклидов алгоритм. Выход будет d = 29.

• Проверьте правильность рассчитанного значения d, рассчитав:

Пусть два простых числа p = 7 и q = 13. Таким образом, модуль n = pq = 7 x 13 = 91.

Выберите e = 5, что является допустимым выбором, поскольку не существует числа с общим множителем 5 и (p — 1) (q — 1) = 6 × 12 = 72, кроме 1.

Пара чисел (n, e) = (91, 5) образует открытый ключ и может быть доступна любому, кому мы хотим отправлять нам зашифрованные сообщения.

Введите p = 7, q = 13 и e = 5 в расширенный евклидов алгоритм. Выход будет d = 29.

Проверьте правильность рассчитанного значения d, рассчитав:

de = 29 × 5 = 145 = 1 mod 72

• Следовательно, открытый ключ (91, 5) и закрытый ключ (91, 29).

Следовательно, открытый ключ (91, 5) и закрытый ключ (91, 29).

Шифрование и дешифрование

Как только пара ключей была сгенерирована, процесс шифрования и дешифрования относительно прост и вычислительно прост.

Интересно, что RSA не работает напрямую со строками битов, как в случае шифрования с симметричным ключом. Он работает по номерам по модулю n. Следовательно, необходимо представлять открытый текст в виде последовательности чисел, меньшей n.

RSA шифрование

• Предположим, отправитель хочет отправить текстовое сообщение тому, чей открытый ключ (n, e).

• Затем отправитель представляет открытый текст в виде последовательности чисел, меньшей n.

• Для шифрования первого открытого текста P, который является числом по модулю n. Процесс шифрования является простым математическим шагом, так как —

Предположим, отправитель хочет отправить текстовое сообщение тому, чей открытый ключ (n, e).

Затем отправитель представляет открытый текст в виде последовательности чисел, меньшей n.

Для шифрования первого открытого текста P, который является числом по модулю n. Процесс шифрования является простым математическим шагом, так как —

C = P e mod n

• Другими словами, зашифрованный текст C равен открытому тексту P, умноженному на него e раз, а затем уменьшенному по модулю n. Это означает, что C также число меньше n.

• Возвращаясь к нашему примеру генерации ключей с открытым текстом P = 10, мы получаем зашифрованный текст C —

Другими словами, зашифрованный текст C равен открытому тексту P, умноженному на него e раз, а затем уменьшенному по модулю n. Это означает, что C также число меньше n.

Возвращаясь к нашему примеру генерации ключей с открытым текстом P = 10, мы получаем зашифрованный текст C —

C = 10 5 mod 91

Расшифровка RSA

• Процесс дешифрования для RSA также очень прост. Предположим, что получатель пары открытого ключа (n, e) получил зашифрованный текст C.

• Получатель поднимает C до уровня своего личного ключа d. Результат по модулю n будет открытым текстом P.

Процесс дешифрования для RSA также очень прост. Предположим, что получатель пары открытого ключа (n, e) получил зашифрованный текст C.

Получатель поднимает C до уровня своего личного ключа d. Результат по модулю n будет открытым текстом P.

Plaintext = C d mod n

• Возвращаясь снова к нашему числовому примеру, зашифрованный текст C = 82 расшифровывается до номера 10 с использованием закрытого ключа 29 —

Возвращаясь снова к нашему числовому примеру, зашифрованный текст C = 82 расшифровывается до номера 10 с использованием закрытого ключа 29 —

Plaintext = 82 29 mod 91 = 10

Анализ RSA

Безопасность RSA зависит от сильных сторон двух отдельных функций. Криптосистема RSA является самой популярной криптосистемой с открытым ключом, сила которой основана на практической сложности факторизации очень больших чисел.

• Функция шифрования — рассматривается как односторонняя функция преобразования открытого текста в зашифрованный текст, и ее можно обратить только с помощью знания закрытого ключа d.

• Генерация ключа . Сложность определения личного ключа из открытого ключа RSA эквивалентна факторизации модуля n. Таким образом, злоумышленник не может использовать знание открытого ключа RSA для определения закрытого ключа RSA, если он не может указать n. Это также односторонняя функция, переход от значений p & q к модулю n прост, но обратный процесс невозможен.

Функция шифрования — рассматривается как односторонняя функция преобразования открытого текста в зашифрованный текст, и ее можно обратить только с помощью знания закрытого ключа d.

Генерация ключа . Сложность определения личного ключа из открытого ключа RSA эквивалентна факторизации модуля n. Таким образом, злоумышленник не может использовать знание открытого ключа RSA для определения закрытого ключа RSA, если он не может указать n. Это также односторонняя функция, переход от значений p & q к модулю n прост, но обратный процесс невозможен.

Если любая из этих двух функций окажется не односторонней, RSA будет нарушен. Фактически, если будет разработана методика эффективного факторинга, RSA больше не будет безопасным.

Сила шифрования RSA резко снижается против атак, если числа p и q не являются большими простыми числами и / или выбранный открытый ключ e является небольшим числом.

Эль-Гамальская криптосистема

Наряду с RSA предлагаются и другие криптосистемы с открытым ключом. Многие из них основаны на разных версиях проблемы дискретного логарифма.

Криптосистема Эль-Гамаля, называемая вариантом эллиптической кривой, основана на задаче дискретного логарифма. Он получает силу из предположения, что дискретные логарифмы не могут быть найдены в практических временных рамках для данного числа, в то время как обратная операция мощности может быть вычислена эффективно.

Давайте рассмотрим простую версию ElGamal, которая работает с числами по модулю p. В случае вариантов эллиптической кривой она основана на совершенно разных системах счисления.

Генерация пары ключей Эль-Гамаля

Каждый пользователь криптосистемы ElGamal генерирует пару ключей следующим образом:

• Выбор большого простого числа p. Обычно выбирается простое число длиной от 1024 до 2048 бит.

• Выбор элемента генератора g.

  • Это число должно быть от 1 до p — 1, но не может быть любым числом.

  • Это генератор мультипликативной группы целых чисел по модулю p. Это означает, что для любого целого числа m, взаимно простого с p, существует такое целое число k, что g ^k = a mod n.

    Например, 3 является генератором группы 5 (Z ₅ = {1, 2, 3, 4}).

Выбор большого простого числа p. Обычно выбирается простое число длиной от 1024 до 2048 бит.

Выбор элемента генератора g.

Это число должно быть от 1 до p — 1, но не может быть любым числом.

Это генератор мультипликативной группы целых чисел по модулю p. Это означает, что для любого целого числа m, взаимно простого с p, существует такое целое число k, что g ^k = a mod n.

Например, 3 является генератором группы 5 (Z ₅ = {1, 2, 3, 4}).

N	3 н	3 n мод 5
1	3	3
2	9	4
3	27	2
4	81	1

• Выбор закрытого ключа. Закрытый ключ x — это любое число больше 1 и меньше p − 1.

• Вычислительная часть открытого ключа. Значение y вычисляется из параметров p, g и закрытого ключа x следующим образом:

Выбор закрытого ключа. Закрытый ключ x — это любое число больше 1 и меньше p − 1.

Вычислительная часть открытого ключа. Значение y вычисляется из параметров p, g и закрытого ключа x следующим образом:

y = g x mod p

• Получение открытого ключа. Открытый ключ Эль-Гамаля состоит из трех параметров (p, g, y).

  Например, предположим, что p = 17 и g = 6 (можно подтвердить, что 6 является генератором группы Z ₁₇ ). Закрытый ключ x может быть любым числом больше 1 и меньше 71, поэтому мы выбираем x = 5. Затем значение y вычисляется следующим образом:

Получение открытого ключа. Открытый ключ Эль-Гамаля состоит из трех параметров (p, g, y).

Например, предположим, что p = 17 и g = 6 (можно подтвердить, что 6 является генератором группы Z ₁₇ ). Закрытый ключ x может быть любым числом больше 1 и меньше 71, поэтому мы выбираем x = 5. Затем значение y вычисляется следующим образом:

y = 6 5 mod 17 = 7

• Таким образом, закрытый ключ равен 62, а открытый ключ — (17, 6, 7).

Таким образом, закрытый ключ равен 62, а открытый ключ — (17, 6, 7).

Шифрование и дешифрование

Генерирование пары ключей Эль-Гамаля сравнительно проще, чем эквивалентный процесс для RSA. Но шифрование и дешифрование немного сложнее, чем RSA.

Эль-Гамаль Шифрование

Предположим, отправитель желает отправить открытый текст кому-то, чей открытый ключ ElGamal (p, g, y), затем —

• Отправитель представляет собой открытый текст в виде последовательности чисел по модулю p.

• Для шифрования первого открытого текста P, который представлен в виде числа по модулю p. Процесс шифрования для получения зашифрованного текста C выглядит следующим образом:

  • Произвольно сгенерировать число k;
  • Вычислить два значения С1 и С2, где —

Отправитель представляет собой открытый текст в виде последовательности чисел по модулю p.

Для шифрования первого открытого текста P, который представлен в виде числа по модулю p. Процесс шифрования для получения зашифрованного текста C выглядит следующим образом:

C1 = g k mod p
C2 = (P * y k ) mod p

• Отправьте зашифрованный текст C, состоящий из двух отдельных значений (C1, C2), отправленных вместе.

• Ссылаясь на наш пример генерации ключей Эль-Гамаля, приведенный выше, открытый текст P = 13 шифруется следующим образом:

  • Произведите случайное число, скажем, к = 10
  • Вычислить два значения С1 и С2, где —

Отправьте зашифрованный текст C, состоящий из двух отдельных значений (C1, C2), отправленных вместе.

Ссылаясь на наш пример генерации ключей Эль-Гамаля, приведенный выше, открытый текст P = 13 шифруется следующим образом:

C1 = 6 10 mod 17
C2 = (13 * 7 10 ) mod 17 = 9

• Отправьте зашифрованный текст C = (C1, C2) = (15, 9).

Отправьте зашифрованный текст C = (C1, C2) = (15, 9).

Эль-Гамальская расшифровка

• Чтобы расшифровать зашифрованный текст (C1, C2) с помощью закрытого ключа x, предпринимаются следующие два шага:

  • Вычислить модульную обратную величину (C1) ^x по модулю p, которая равна (C1) ^-x , обычно называемому коэффициентом дешифрования.

  • Получите открытый текст, используя следующую формулу —

Чтобы расшифровать зашифрованный текст (C1, C2) с помощью закрытого ключа x, предпринимаются следующие два шага:

Вычислить модульную обратную величину (C1) ^x по модулю p, которая равна (C1) ^-x , обычно называемому коэффициентом дешифрования.

Получите открытый текст, используя следующую формулу —

C2 × (C1) -x  mod p = Plaintext

• В нашем примере для расшифровки зашифрованного текста C = (C1, C2) = (15, 9) с использованием закрытого ключа x = 5 коэффициент дешифрования равен

В нашем примере для расшифровки зашифрованного текста C = (C1, C2) = (15, 9) с использованием закрытого ключа x = 5 коэффициент дешифрования равен

15 -5  mod 17 = 9

• Извлечь открытый текст P = (9 × 9) мод 17 = 13.

Извлечь открытый текст P = (9 × 9) мод 17 = 13.

Эль-Гамаль Анализ

В системе ElGamal каждый пользователь имеет закрытый ключ x. и имеет три компонента открытого ключа — простой модуль p, генератор g и открытый Y = g ^x mod p . Сила Эль-Гамаля основана на сложности проблемы дискретного логарифма.

Размер безопасного ключа обычно> 1024 бит. Сегодня используется даже ключ длиной 2048 бит. Что касается скорости обработки, Elgamal довольно медленный, он используется в основном для протоколов аутентификации ключей. Из-за более высокой эффективности обработки варианты ElGamal с эллиптической кривой становятся все более популярными.

Криптография с эллиптической кривой (ECC)

Криптография с эллиптической кривой (ECC) — это термин, используемый для описания набора криптографических инструментов и протоколов, безопасность которых основана на специальных версиях проблемы дискретного логарифма. Он не использует числа по модулю p.

ECC основан на наборах чисел, которые связаны с математическими объектами, называемыми эллиптическими кривыми. Существуют правила сложения и вычисления кратных этих чисел, так же как и для чисел по модулю p.

ECC включает в себя варианты многих криптографических схем, которые изначально были разработаны для модульных номеров, таких как шифрование Эль-Гамаля и алгоритм цифровой подписи.

Считается, что проблема дискретного логарифма гораздо сложнее, когда она применяется к точкам на эллиптической кривой. Это побуждает переключаться с чисел по модулю p на точки на эллиптической кривой. Также эквивалентный уровень безопасности может быть получен с помощью более коротких ключей, если мы используем варианты на основе эллиптических кривых.

Более короткие ключи дают два преимущества:

• Простота управления ключами
• Эффективные вычисления

Эти преимущества делают варианты схемы шифрования на основе эллиптических кривых весьма привлекательными для приложений, где вычислительные ресурсы ограничены.

Схемы RSA и Эль-Гамаля — Сравнение

Давайте кратко сравним схемы RSA и Эль-Гамаля по различным аспектам.