В этом разделе мы представляем некоторые продвинутые темы по генетическим алгоритмам. Читатель, ищущий просто введение в ГА, может пропустить этот раздел.
Ограниченные проблемы оптимизации
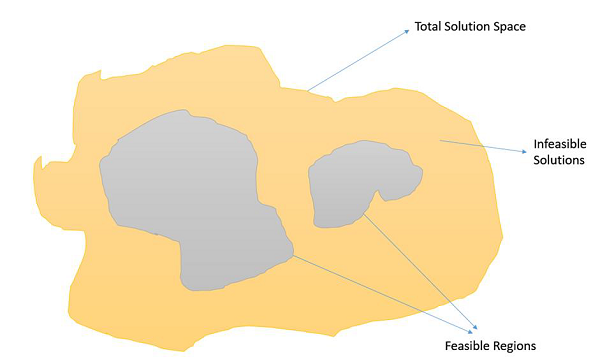
Ограниченные проблемы оптимизации — это те проблемы оптимизации, в которых мы должны максимизировать или минимизировать заданное значение целевой функции, на которое распространяются определенные ограничения. Следовательно, не все результаты в пространстве решений достижимы, и пространство решений содержит допустимые области, как показано на следующем рисунке.
В таком случае операторы кроссовера и мутации могут дать нам решения, которые неосуществимы. Поэтому при работе с ограниченными задачами оптимизации необходимо использовать дополнительные механизмы в GA.
Некоторые из наиболее распространенных методов —
-
Использование штрафных функций, которые уменьшают пригодность невыполнимых решений, предпочтительно, чтобы пригодность уменьшалась пропорционально количеству нарушенных ограничений или расстоянию от допустимой области.
-
Использование функций восстановления, которые принимают недопустимое решение и модифицируют его так, чтобы нарушенные ограничения были удовлетворены.
-
Не допускать попадания неосуществимых решений в население.
-
Используйте специальные функции представления или декодирования, которые обеспечивают выполнимость решений.
Использование штрафных функций, которые уменьшают пригодность невыполнимых решений, предпочтительно, чтобы пригодность уменьшалась пропорционально количеству нарушенных ограничений или расстоянию от допустимой области.
Использование функций восстановления, которые принимают недопустимое решение и модифицируют его так, чтобы нарушенные ограничения были удовлетворены.
Не допускать попадания неосуществимых решений в население.
Используйте специальные функции представления или декодирования, которые обеспечивают выполнимость решений.
Основные теоретические основы
В этом разделе мы обсудим теорему Схемы и НФЛ вместе с гипотезой строительного блока.
Схема Теорема
Исследователи пытаются выяснить математику, лежащую в основе работы генетических алгоритмов, и теорема о схеме Голландии является шагом в этом направлении. В течение года были внесены различные улучшения и предложения в теорему схемы, чтобы сделать ее более общей.
В этом разделе мы не углубляемся в математику теоремы схемы, а скорее пытаемся развить базовое понимание того, что такое теорема схемы. Основная терминология, которую нужно знать, такова:
-
Схема — это «шаблон». Формально это строка над алфавитом = {0,1, *},
где * не волнует и может принимать любое значение.
Следовательно, * 10 * 1 может означать 01001, 01011, 11001 или 11011.
Геометрически схема является гиперплоскостью в пространстве поиска решения.
-
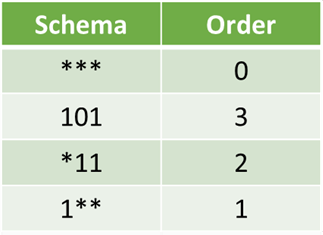
Порядок схемы — это количество указанных фиксированных позиций в гене.
Схема — это «шаблон». Формально это строка над алфавитом = {0,1, *},
где * не волнует и может принимать любое значение.
Следовательно, * 10 * 1 может означать 01001, 01011, 11001 или 11011.
Геометрически схема является гиперплоскостью в пространстве поиска решения.
Порядок схемы — это количество указанных фиксированных позиций в гене.
-
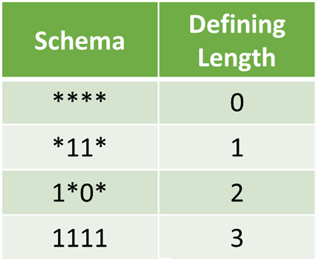
Определение длины — это расстояние между двумя самыми дальними фиксированными символами в гене.
Определение длины — это расстояние между двумя самыми дальними фиксированными символами в гене.
Теорема о схеме гласит, что эта схема с пригодностью выше среднего, короткой определяющей длиной и более низким порядком, скорее всего, переживет кроссовер и мутацию.
Гипотеза строительного блока
Строительные блоки представляют собой схемы низкого порядка с низкой определяемой длиной с учетом приведенной выше средней пригодности. Гипотеза о строительном блоке говорит, что такие строительные блоки служат основой для успеха и адаптации ГА в ГА, поскольку она прогрессирует путем последовательной идентификации и рекомбинации таких «строительных блоков».
Нет свободного обеда (НФЛ) Теорема
Wolpert и Macready в 1997 году опубликовали статью под названием «Теоремы об отсутствии бесплатного обеда для оптимизации». По сути, это говорит о том, что если мы усредним по пространству всех возможных проблем, то все не повторяющиеся алгоритмы черного ящика будут демонстрировать одинаковую производительность.
Это означает, что чем больше мы понимаем проблему, наш GA становится более специфичным для проблемы и дает лучшую производительность, но это компенсирует это, выполняя плохо для других проблем.
GA на основе машинного обучения
Генетические алгоритмы также находят применение в машинном обучении. Системы классификаторов — это форма системы машинного обучения на основе генетики (GBML), которая часто используется в области машинного обучения. Методы GBML являются нишевым подходом к машинному обучению.
Есть две категории систем GBML —
-
Подход Питтсбурга — В этом подходе одна хромосома кодировала одно решение, и таким образом пригодность была назначена решениям.
-
Мичиганский подход — одно решение, как правило, представлено многими хромосомами, и поэтому пригодность определяется частичными решениями.
Подход Питтсбурга — В этом подходе одна хромосома кодировала одно решение, и таким образом пригодность была назначена решениям.
Мичиганский подход — одно решение, как правило, представлено многими хромосомами, и поэтому пригодность определяется частичными решениями.
Следует иметь в виду, что стандартные проблемы, такие как кроссовер, мутация, ламарковская или дарвиновская и т. Д., Также присутствуют в системах GBML.