Специальные функции LPF и HPF

Цепи фильтра низких и высоких частот используются в качестве специальных схем во многих приложениях. Фильтр нижних частот (LPF) может работать в качестве интегратора , тогда как фильтр верхних частот (HPF) может работать в качестве дифференциатора . Эти две математические функции возможны только с этими схемами, которые уменьшают усилия инженера-электронщика во многих приложениях.

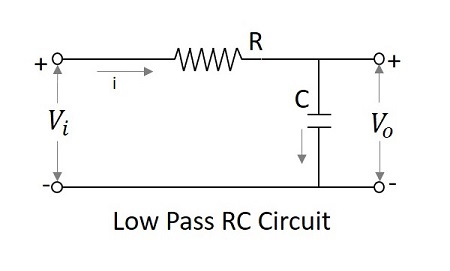
Фильтр низких частот в качестве интегратора

На низких частотах емкостное реактивное сопротивление стремится к бесконечности, а на высоких частотах реактивное сопротивление становится равным нулю. Следовательно, на низких частотах ФНЧ имеет конечный выходной сигнал, а на высоких частотах выходной сигнал равен нулю, что одинаково для интегральной схемы. Следовательно, можно сказать, что фильтр низких частот работает как интегратор .

Для LPF вести себя как интегратор

$$\ tau \ gg T$$

Где $\ tau = RC$ постоянная времени цепи

Тогда изменение напряжения в С очень мало.

Vi=iR+ frac1C intidt $$V_ {i} = iR + \ frac {1} {C} \ int i \: dt$$

$$V_ {i} \ cong iR$$

Since frac1C intidt lliR $$Since \: \: \ frac {1} {C} \ int i \: dt \ ll iR$$

$$I = \ гидроразрыва {V_ {я}} {R}$$

SinceV0= frac1C intidt= frac1RC intVidt= frac1 tau intVidt $$Since \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} \ int V_ {i} dt$$

$$Output \ propto \ int input$$

Следовательно, ФНЧ с большой постоянной времени производит выходной сигнал, который пропорционален интегралу входного сигнала.

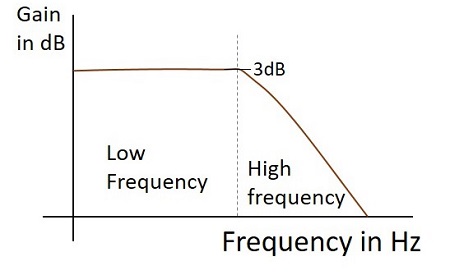
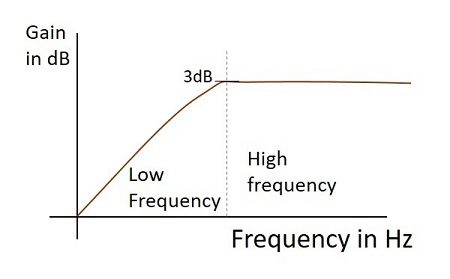
Частотный отклик

Частотная характеристика практического фильтра нижних частот, когда он работает как интегратор, как показано ниже.

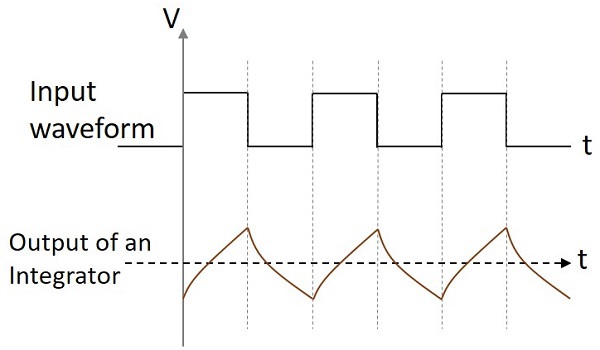
Форма выходного сигнала

Если интегральной схеме дан синусоидальный вход, на выходе будет косинусоидальная волна. Если входной сигнал представляет собой прямоугольную волну, форма выходной волны меняет свою форму и выглядит так, как показано на рисунке ниже.

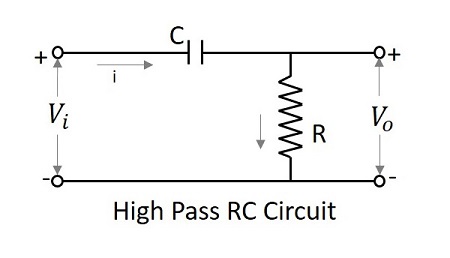
Фильтр верхних частот в качестве дифференциатора

На низких частотах выход дифференциатора равен нулю, тогда как на высоких частотах его выход имеет некоторое конечное значение. Это то же самое, что и для дифференциатора. Следовательно, фильтр верхних частот считается дифференцирующим.

Если постоянная времени RC HPF намного меньше, чем период времени входного сигнала, то схема ведет себя как дифференциатор. Тогда падение напряжения на R очень мало по сравнению с падением на C.

Vi= frac1C intidt+iR $$V_ {i} = \ frac {1} {C} \ int i \: dt + iR$$

Но $iR = V_ {0}$ мало

начинаясVi= frac1C intidt $$начиная с V_ {i} = \ frac {1} {C} \ int i \: dt$$

$$I = \ гидроразрыва {V_ {0}} {R}$$

SinceVi= frac1 tau intV0dt $$Since \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt$$

Где $\ tau = RC$ постоянная времени цепи.

Дифференцируя с обеих сторон,

$$\ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau}$$

$$V_ {0} = \ tau \ frac {dV_ {i}} {dt}$$

SinceV0 propto fracdVidt $$Since \: V_ {0} \ propto \ frac {dV_ {i}} {dt}$$

Выходной сигнал пропорционален разности входного сигнала.

Частотный отклик

Частотная характеристика практического фильтра верхних частот, когда он работает в качестве дифференциатора, как показано ниже.

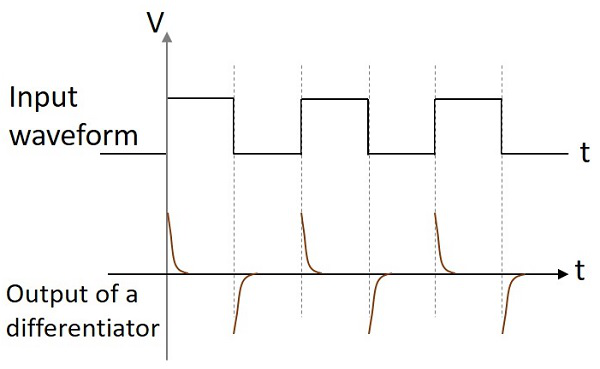
Форма выходной волны

Если цепь дифференциатора получает синусоидальный вход, выходной сигнал будет косинусной волной. Если входной сигнал представляет собой прямоугольную волну, форма выходной волны меняет свою форму и выглядит так, как показано на рисунке ниже.

Эти две схемы в основном используются в различных электронных приложениях. Схема дифференциатора вырабатывает постоянное выходное напряжение, когда входной сигнал имеет тенденцию к постоянному изменению. Схема интегратора вырабатывает стабильно изменяющееся выходное напряжение, когда входное напряжение постоянно.