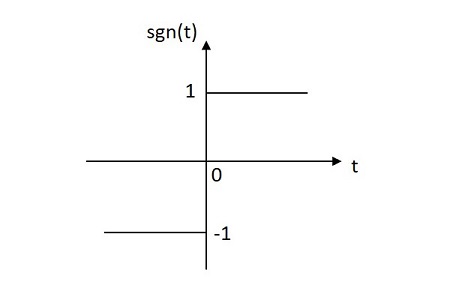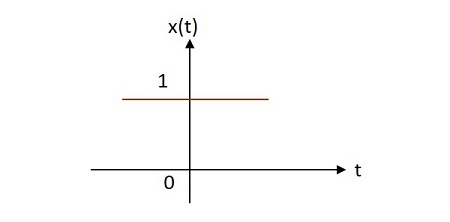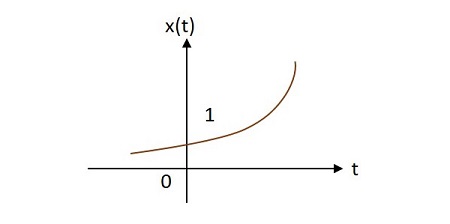Электронные схемы — Сигналы

Сигнал можно понимать как «представление, которое дает некоторую информацию о данных, присутствующих в источнике, из которого они получены». Обычно это время меняется. Следовательно, сигнал может быть источником энергии, который передает некоторую информацию . Это легко можно представить на графике.

Примеры

• Сигнал тревоги дает сигнал, что пришло время.
• Свисток подтверждает, что еда приготовлена.
• Красный свет сигнализирует об опасности.
• Светофор указывает на ваше движение.
• Звонит телефон, сигнализирующий о звонке для вас.

Сигнал может быть любого типа, который передает некоторую информацию. Этот сигнал, производимый электронным оборудованием, называется электронным сигналом или электрическим сигналом . Обычно это временные варианты.

Типы сигналов

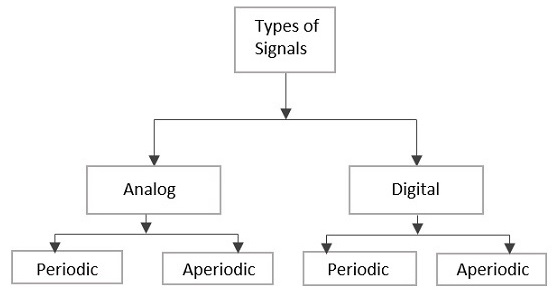
Сигналы могут быть классифицированы как аналоговые или цифровые, в зависимости от их характеристик. Аналоговые и цифровые сигналы могут быть дополнительно классифицированы, как показано на следующем рисунке.

Аналоговый сигнал

Непрерывный изменяющийся во времени сигнал, который представляет изменяющуюся во времени величину, можно назвать аналоговым сигналом . Этот сигнал продолжает изменяться во времени в соответствии с мгновенными значениями величины, которая его представляет.

Цифровой сигнал

Сигнал, который является дискретным по природе или который не является непрерывным по форме, можно назвать цифровым сигналом . Этот сигнал имеет отдельные значения, обозначенные отдельно, которые не основаны на предыдущих значениях, как если бы они были получены в этот конкретный момент времени.

Периодический сигнал и апериодический сигнал

Любой аналоговый или цифровой сигнал, который повторяет свою схему в течение определенного периода времени, называется периодическим сигналом . Этот сигнал постоянно повторяется, и его легко предположить или рассчитать.

Любой аналоговый или цифровой сигнал, который не повторяет своего паттерна в течение определенного периода времени, называется апериодическим сигналом . Этот сигнал имеет свой паттерн продолженным, но паттерн не повторяется, и его не так легко предположить или рассчитать.

Сигналы и нотации

Среди периодических сигналов наиболее часто используемые сигналы — это синусоида, косинусоида, треугольная форма волны, прямоугольная волна, прямоугольная волна, форма зубца пилы, форма импульса или последовательность импульсов и т. Д. Давайте посмотрим на эти формы волны.

Сигнал шага блока

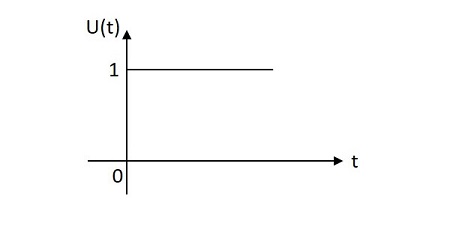
Сигнал единичного шага имеет значение в одну единицу от начала координат до одной единицы на оси X. Это в основном используется в качестве тестового сигнала. Изображение единичного шагового сигнала показано ниже.

Функция единичного шага обозначается как $u \ left (t \ right)$. Определяется как —

$$u \ left (t \ right) = \ left \ {\ begin {matrix} 1 & t \ geq 0 \\ 0 & t <0 \ end {matrix} \ right.$$

Импульсный сигнал блока

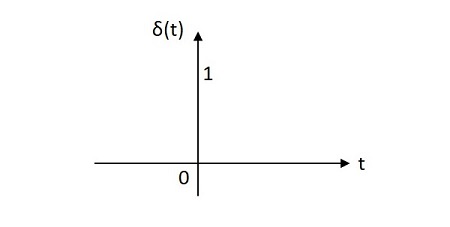
Импульсный сигнал единицы измерения имеет значение одной единицы в своем начале. Его площадь составляет одну единицу. Изображение единичного импульсного сигнала показано ниже.

Функция единичного импульса обозначается через t (t) . Определяется как

$$\ delta \ left (t \ right) = \ left \ {\ begin {matrix} \ infty \: \: if \: \: t = 0 \\ 0 \: \: if \: \: t \ neq 0 \ конец {матрица} \ право.$$

$$\ int _ {- \ infty} ^ {\ infty} \ delta \ left (t \ right) d \ left (t \ right) = 1$$

$$\ int _ {- \ infty} ^ {t} \ delta \ left (t \ right) d \ left (t \ right) = u \ left (t \ right)$$

$$\ delta \ left (t \ right) = \ frac {du \ left (t \ right)} {d \ left (t \ right)}$$

Сигнал рампы

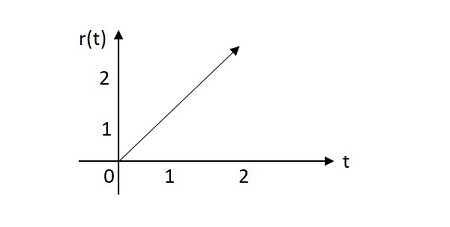
Сигнал линейного изменения имеет экспоненциально возрастающую величину от своего источника. Изображение единичного линейного сигнала показано ниже.

Функция линейного изменения обозначается как u (t) . Определяется как —

$$\ int_ {0} ^ {t} u \ left (t \ right) d \ left (t \ right) = \ int_ {0} ^ {t} 1 dt = t = r \ left (t \ right)$$

$$u \ left (t \ right) = \ frac {dr \ left (t \ right)} {dt}$$

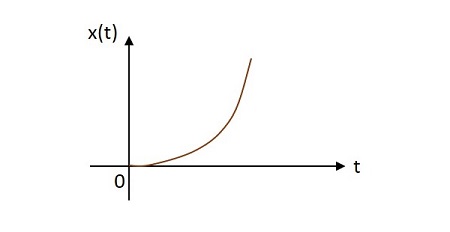
Единичный параболический сигнал

Единичный параболический сигнал имеет свое значение, изменяющееся как парабола в своем источнике. Изображение единичного параболического сигнала показано ниже.

Единичная параболическая функция обозначается через $u \ left (t \ right)$. Определяется как —

$$\ int_ {0} ^ {t} \ int_ {0} ^ {t} u \ left (t \ right) dtdt = \ int_ {0} ^ {t} r \ left (t \ right) dt = \ int_ {0} ^ {t} t.dt = \ frac {t ^ {2}} {2} dt = x \ left (t \ right)$$

$$r \ left (t \ right) = \ frac {dx \ left (t \ right)} {dt}$$

$$u \ left (t \ right) = \ frac {d ^ {2} x \ left (t \ right)} {dt ^ {2}}$$

Функция Signum

Функция Signum имеет свое значение, равномерно распределенное как в положительной, так и в отрицательной плоскостях от ее происхождения. Изображение функции Signum показано ниже.

Функция Signum обозначается как sgn (t) . Определяется как

$$sgn \ left (t \ right) = \ left \ {\ begin {matrix} 1 \: \: для \: \: t \ geq 0 \\ - 1 \: \: для \: \: t <0 \ конец {матрица} \ право.$$

$$sgn \ left (t \ right) = 2u \ left (t \ right) -1$$

Экспоненциальный сигнал

Экспоненциальный сигнал имеет свое значение, экспоненциально отличающееся от его источника. Экспоненциальная функция имеет вид —

$$x \ left (t \ right) = e ^ {\ alpha t}$$

Форма экспоненты может быть определена как $\ alpha$. Эту функцию можно понять в 3 случаях

Случай 1 —

Если $\ alpha = 0 \ rightarrow x \ left (t \ right) = e ^ {0} = 1$

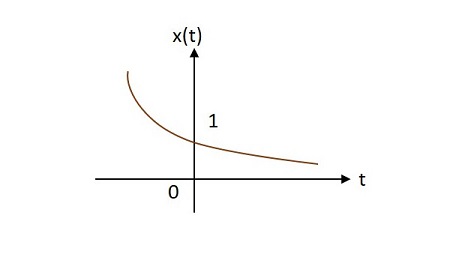
Случай 2 —

Если $\ alpha <0$, то $x \ left (t \ right) = e ^ {\ alpha t}$, где $\ alpha$ отрицательно. Эта форма называется убывающей экспоненциальной .

Дело 3 —

Если $\ alpha> 0$, то $x \ left (t \ right) = e ^ {\ alpha t}$, где $\ alpha$ положительно. Эта форма называется экспоненциальной .

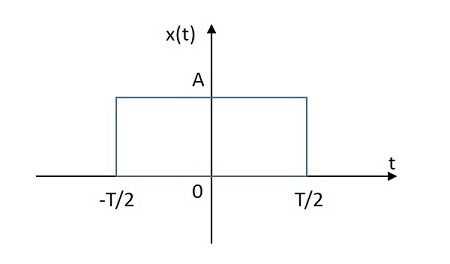
Прямоугольный сигнал

Прямоугольный сигнал имеет свое значение, распределенное в прямоугольной форме в положительной и отрицательной плоскостях от его происхождения. Изображение прямоугольного сигнала показано ниже.

Прямоугольная функция обозначается через $x \ left (t \ right)$. Определяется как

x left(t right)=Arect left[ fractT right] $$x \ left (t \ right) = A \: rect \ left [\ frac {t} {T} \ right]$$

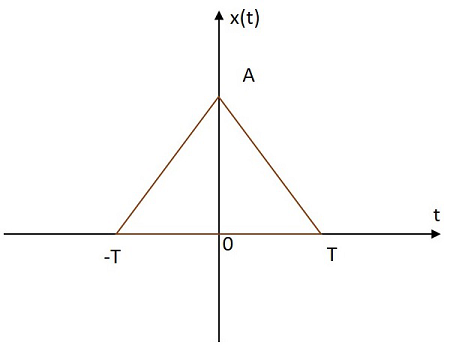
Треугольный сигнал

Прямоугольный сигнал имеет свое значение, распределенное в треугольной форме в положительной и отрицательной плоскостях от его происхождения. Изображение треугольного сигнала показано ниже.

Треугольная функция обозначается через $x \ left (t \ right)$. Определяется как

$$ x \ left (t \ right) = A \ left [1- \ frac {\ left | t \ right |} {T} \ right] $$

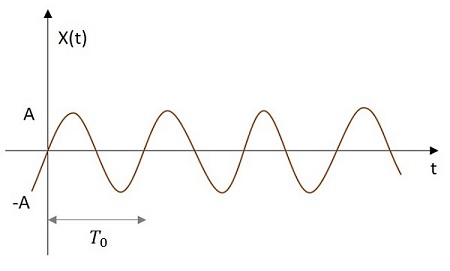
Синусоидальный сигнал

Синусоидальный сигнал имеет синусоидальное значение от источника. Изображение синусоидального сигнала показано ниже.

Синусоидальная функция обозначается через x (t). Определяется как —

$$x \ left (t \ right) = A \ cos \ left (w_ {0} t \ pm \ phi \ right)$$

или же

$$x \ left (t \ right) = грех \ left (w_ {0} t \ pm \ phi \ right)$$

Где $T_ {0} = \ frac {2 \ pi} {w_ {0}}$

Sinc Function

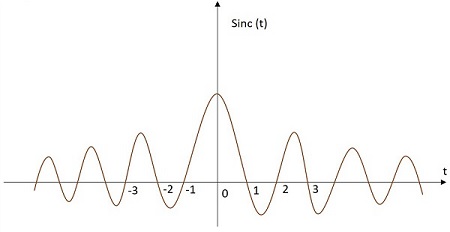
Сигнал Sinc имеет свое значение, изменяющееся в зависимости от конкретного соотношения, как в приведенном ниже уравнении. Он имеет максимальное значение в начале координат и продолжает уменьшаться по мере удаления. Изображение сигнала функции Sinc показано ниже.

Функция Sinc обозначается через sinc (t) . Определяется как —

$$sinc \ left (t \ right) = \ frac {sin \ left (\ pi t \ right)} {\ pi t}$$

Итак, это разные сигналы, с которыми мы в основном сталкиваемся в области электроники и коммуникаций. Каждый сигнал может быть определен в математическом уравнении, чтобы облегчить анализ сигнала.

Каждый сигнал имеет определенную форму волны, как упоминалось ранее. Формирование волны может изменить содержание, присутствующее в сигнале. В любом случае, инженером-конструктором принимается решение, изменять ли волну или нет для какой-либо конкретной цепи. Но, чтобы изменить форму волны, есть несколько методов, которые будут обсуждаться в следующих разделах.