В большинстве случаев мы используем наборы данных, которые содержат несколько количественных переменных, и цель анализа часто состоит в том, чтобы связать эти переменные друг с другом. Это можно сделать через линии регрессии.
При построении регрессионных моделей мы часто проверяем мультиколлинеарность, где нам приходилось видеть корреляцию между всеми комбинациями непрерывных переменных, и предпринимаем необходимые действия для удаления мультиколлинеарности, если она существует. В таких случаях помогает следующая техника.
Функции для рисования моделей линейной регрессии
В Seaborn есть две основные функции для визуализации линейных отношений, определенных посредством регрессии. Этими функциями являются regplot () и lmplot () .
регплот против лмплота
| regplot | lmplot |
|---|---|
| принимает переменные x и y в различных форматах, включая простые числовые массивы, объекты серии pandas или как ссылки на переменные в DataFrame pandas | имеет данные в качестве обязательного параметра, а переменные x и y должны быть указаны в виде строк. Этот формат данных называется «длинные данные» |
Давайте теперь нарисуем графики.
пример
Построение regplot и затем lmplot с теми же данными в этом примере
import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
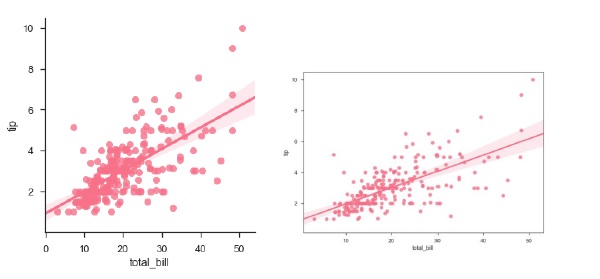
sb.regplot(x = "total_bill", y = "tip", data = df)
sb.lmplot(x = "total_bill", y = "tip", data = df)
plt.show()
Выход
Вы можете увидеть разницу в размере между двумя участками.
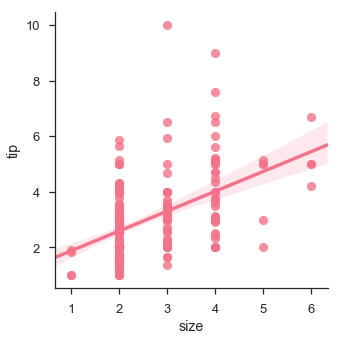
Мы также можем подогнать линейную регрессию, когда одна из переменных принимает дискретные значения
пример
import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
sb.lmplot(x = "size", y = "tip", data = df)
plt.show()
Выход
Подгонка разных видов моделей
Простая модель линейной регрессии, использованная выше, очень проста в подборе, но в большинстве случаев данные являются нелинейными, и вышеуказанные методы не могут обобщить линию регрессии.
Давайте использовать набор данных Анскомба с графиками регрессии —
пример
import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
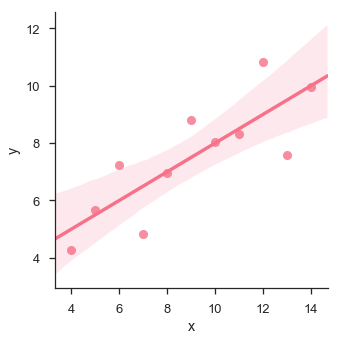
sb.lmplot(x="x", y="y", data=df.query("dataset == 'I'"))
plt.show()
В этом случае данные хорошо подходят для модели линейной регрессии с меньшей дисперсией.
Давайте посмотрим на другой пример, где данные принимают большое отклонение, которое показывает, что линия наилучшего соответствия не является хорошей.
пример
import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
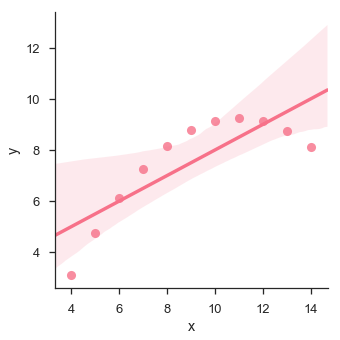
sb.lmplot(x = "x", y = "y", data = df.query("dataset == 'II'"))
plt.show()
Выход
График показывает высокое отклонение точек данных от линии регрессии. Такие нелинейные, более высокого порядка могут быть визуализированы с помощью lmplot () и regplot (). Они могут соответствовать модели полиномиальной регрессии для изучения простых видов нелинейных трендов в наборе данных —