Спутниковая связь — законы Кеплера

Мы знаем, что спутник вращается вокруг Земли, которая похожа на Землю вращается вокруг Солнца. Таким образом, принципы, которые применяются к Земле и ее движению вокруг Солнца, также применимы к спутнику и его движению вокруг Земли.

Многие ученые давали различные типы теорий с ранних времен. Но только Иоганн Кеплер (1571-1630) был одним из наиболее признанных ученых в описании принципа движения спутника вокруг Земли.

Кеплер сформулировал три закона, которые изменили всю теорию спутниковой связи и наблюдения. Они широко известны как законы Кеплера . Они полезны для визуализации движения в пространстве.

Первый закон Кеплера

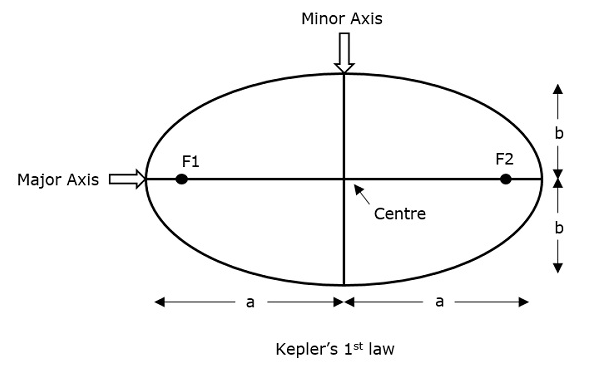
Первый закон Кеплера гласит, что путь, по которому идет спутник вокруг его первичной (Земли), будет эллипсом . Этот эллипс имеет две фокусные точки (фокусы) F1 и F2, как показано на рисунке ниже. Центр масс Земли всегда будет присутствовать в одном из двух фокусов эллипса.

Если рассматривать расстояние от центра объекта до точки на его эллиптической траектории, то самая дальняя точка эллипса от центра называется апогеем, а самая короткая точка эллипса от центра называется перигеем .

Эксцентриситет «е» этой системы можно записать как —

$$e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a}$$

Где a & b — длины большой полуоси и малой оси эллипса соответственно.

Для эллиптического пути значение эксцентриситета (e) всегда лежит в диапазоне от 0 до 1, то есть $0$ < $e$ < $1$ , поскольку a больше, чем b. Предположим, что если значение эксцентриситета (e) равно нулю, то траектория больше не будет иметь эллиптической формы, скорее она будет преобразована в круглую форму.

Второй закон Кеплера

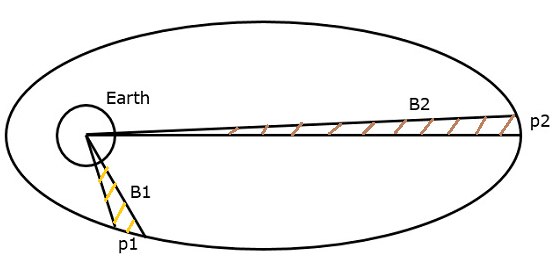
Второй закон Кеплера гласит, что в течение равных промежутков времени площадь, охватываемая спутником, будет одинаковой по отношению к центру масс Земли. Это можно понять, взглянув на следующий рисунок.

Предположим, что спутник покрывает расстояния p1 и p2 в одном и том же интервале времени. Тогда области B1 и B2, охватываемые спутником в этих двух случаях, равны.

Третий закон Кеплера

Третий закон Кеплера гласит, что квадрат периодического времени эллиптической орбиты пропорционален кубу длины его большой полуоси. Математически это можно записать следующим образом:

T2 альфаа3 $$T ^ 2 \: \ альфа \: а ^ 3$$

$$=&amp;gt; T ^ 2 = \ left (\ frac {4 \ pi ^ 2} {\ mu} \ right) a ^ 3$$

Где $\ frac {4 \ pi ^ 2} {\ mu}$ — константа пропорциональности.

$\ mu$ — постоянная Кеплера, и ее значение равно 3.986005 x 10 ¹⁴ м ³ / с ²

$$1 = \ left (\ frac {2 \ pi} {T} \ right) ^ 2 \ left (\ frac {a ^ 2} {\ mu} \ right)$$

$$1 = n ^ 2 \ left (\ frac {a ^ 3} {\ mu} \ right)$$

$$=&amp;gt; a ^ 3 = \ frac {\ mu} {n ^ 2}$$

Где ‘n’ — среднее движение спутника в радианах в секунду.

Примечание . Спутник, когда он вращается вокруг Земли, подвергается воздействию силы притяжения от Земли, которая является силой гравитации. Точно так же он испытывает другую силу тяги от солнца и луны. Поэтому спутник должен уравновесить эти две силы, чтобы удержаться на своей орбите.