Мы знаем, что путь спутника, вращающегося вокруг Земли, известен как орбита . Этот путь может быть представлен с помощью математических обозначений. Орбитальная механика — это исследование движения спутников, присутствующих на орбитах. Таким образом, мы можем легко понять космические операции со знанием орбитального движения.
Орбитальные Элементы
Орбитальные элементы — это параметры, которые полезны для описания орбитального движения спутников. Ниже приведены орбитальные элементы .
- Большая полуось
- эксцентричность
- Средняя аномалия
- Аргумент перигея
- наклонение
- Прямое восхождение на восходящий узел
Вышеупомянутые шесть орбитальных элементов определяют орбиту земных спутников. Следовательно, легко отличить один спутник от других спутников на основе значений орбитальных элементов.
Большая полуось
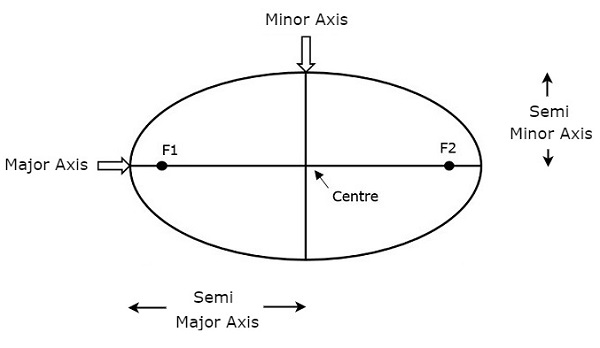
Длина большой полуоси (а) определяет размер орбиты спутника. Это половина большой оси. Это проходит от центра через фокус к краю эллипса. Таким образом, это радиус орбиты в двух самых удаленных точках орбиты.
Обе полуоси и полуоси представлены на рисунке выше. Длина большой полуоси (а) определяет не только размер орбиты спутника, но и период обращения.
Если круговая орбита рассматривается как особый случай, то длина большой полуоси будет равна радиусу этой круговой орбиты.
эксцентричность
Значение эксцентриситета (e) фиксирует форму орбиты спутника. Этот параметр указывает на отклонение формы орбиты от идеального круга.
Если длины большой полуоси и малой оси эллиптической орбиты являются a & b, то математическое выражение для эксцентриситета (e) будет
$$ e = \ frac {\ sqrt {a ^ 2 — b ^ 2}} {a} $$
Значение эксцентриситета круговой орбиты равно нулю , так как оба a и b равны. Принимая во внимание, что значение эксцентриситета эллиптической орбиты лежит между нулем и единицей.
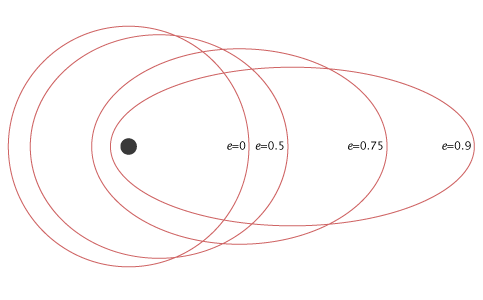
На следующем рисунке показаны различные спутниковые орбиты для разных значений эксцентриситета (e).
На приведенном выше рисунке спутниковая орбита, соответствующая нулевому значению эксцентриситета (e), является круговой орбитой. И остальные три спутниковые орбиты имеют эллиптическую форму, соответствующую значениям эксцентриситета (e) 0,5, 0,75 и 0,9.
Средняя аномалия
Для спутника точка, ближайшая к Земле, называется Перигеем. Средняя аномалия (М) дает среднее значение углового положения спутника относительно перигея.
Если орбита круглая, то средняя аномалия дает угловое положение спутника на орбите. Но если орбита эллиптическая, то вычисление точного положения очень сложно. В это время средняя аномалия используется в качестве промежуточного шага.
Аргумент Перигея
Спутниковая орбита разрезает экваториальную плоскость в двух точках. Первая точка называется нисходящим узлом , где спутник проходит от северного полушария к южному полушарию. Вторая точка называется восходящим узлом , где спутник проходит от южного полушария к северному полушарию.
Аргумент перигея (ω) — угол между восходящим узлом и перигеем. Если и перигей, и восходящий узел существуют в одной и той же точке, то аргумент перигея будет равен нулю
Аргумент перигея измеряется в плоскости орбиты в центре Земли в направлении движения спутника.
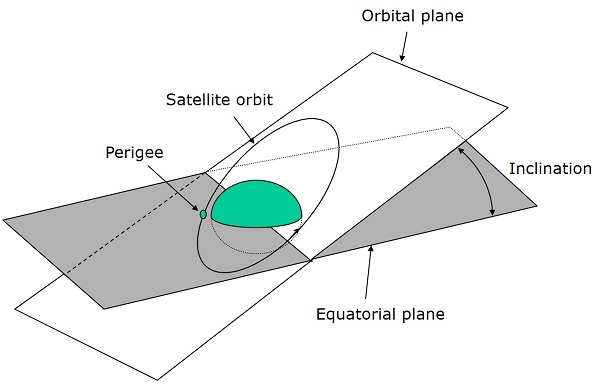
наклонение
Угол между плоскостью орбиты и экваториальной плоскостью Земли известен как наклон (i) . Он измеряется в восходящем узле с направлением с востока на север. Таким образом, наклон определяет ориентацию орбиты, рассматривая экватор Земли в качестве ориентира.
Есть четыре типа орбит, основанных на угле наклона.
-
Экваториальная орбита — угол наклона равен нулю или 180 градусам.
-
Полярная орбита — угол наклона 90 градусов.
-
Поворотная орбита — Угол наклона лежит от нуля до 90 градусов.
-
Ретроградная орбита — угол наклона составляет от 90 до 180 градусов.
Экваториальная орбита — угол наклона равен нулю или 180 градусам.
Полярная орбита — угол наклона 90 градусов.
Поворотная орбита — Угол наклона лежит от нуля до 90 градусов.
Ретроградная орбита — угол наклона составляет от 90 до 180 градусов.
Прямое Вознесение Восходящего Узла
Мы знаем, что восходящий узел — это точка, где спутник пересекает экваториальную плоскость при переходе от южного полушария к северному полушарию.
Прямое восхождение восходящего узла (Ω) — это угол между линией Овна и восходящим узлом в восточном направлении в экваториальной плоскости. Овен также называют весенним и равноденственным.
Наземный трек спутника — это путь на поверхности Земли, которая лежит точно под его орбитой. Наземный трек спутника может принимать различные формы в зависимости от значений орбитальных элементов.
Орбитальные уравнения
В этом разделе мы обсудим уравнения, связанные с орбитальным движением.
Силы, действующие на спутник
Спутник, когда он вращается вокруг Земли, подвергается притягивающей силе от Земли из-за гравитационной силы Земли. Эта сила известна как центростремительная сила (F 1 ), потому что эта сила стремится к спутнику к нему.
Математически центростремительная сила (F 1 ), действующая на спутник из-за земли, может быть записана как
$$ F_ {1} = \ frac {GMm} {R ^ 2} $$
Куда,
-
G — универсальная гравитационная постоянная, и она равна 6,673 x 10 -11 Н ∙ м 2 / кг 2 .
-
М — масса земли, и она равна 5,98 х 10 24 кг.
-
м — масса спутника.
-
R — расстояние от спутника до центра Земли.
G — универсальная гравитационная постоянная, и она равна 6,673 x 10 -11 Н ∙ м 2 / кг 2 .
М — масса земли, и она равна 5,98 х 10 24 кг.
м — масса спутника.
R — расстояние от спутника до центра Земли.
Спутник, когда он вращается вокруг Земли, подвергается воздействию силы притяжения Солнца и Луны из-за их гравитационных сил. Эта сила известна как центробежная сила (F 2 ), потому что эта сила уводит спутник от земли.
Математически, центробежная сила (F 2 ), действующая на спутник, может быть записана как
$$ F_ {2} = \ frac {mv ^ 2} {R} $$
Где v — орбитальная скорость спутника.
Орбитальная скорость
Орбитальная скорость спутника — это скорость, с которой спутник вращается вокруг Земли. Спутник не отклоняется от своей орбиты и движется с определенной скоростью на этой орбите, когда центростремительные и центробежные силы уравновешивают друг друга.
Итак, приравниваем центростремительную силу (F 1 ) и центробежную силу (F 2 ).
$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $$
$$ => \ frac {GM} {R} = v ^ 2 $$
$$ => v = \ sqrt {\ frac {GM} {R}} $$
Следовательно, орбитальная скорость спутника равна
$$ v = \ sqrt {\ frac {GM} {R}} $$
Куда,
-
G — гравитационная постоянная, и она равна 6,673 x 10 -11 Н ∙ м 2 / кг 2 .
-
М — масса земли, и она равна 5,98 х 10 24 кг.
-
R — расстояние от спутника до центра Земли.
G — гравитационная постоянная, и она равна 6,673 x 10 -11 Н ∙ м 2 / кг 2 .
М — масса земли, и она равна 5,98 х 10 24 кг.
R — расстояние от спутника до центра Земли.
Таким образом, орбитальная скорость в основном зависит от расстояния от спутника до центра Земли (R), поскольку G & M являются постоянными.