Лямбда-исчисление — это структура, разработанная Алонзо Черчем в 1930-х годах для изучения вычислений с функциями.
-
Создание функции — Черч ввел обозначение λx.E для обозначения функции, в которой «x» является формальным аргументом, а «E» — функциональным телом. Эти функции могут быть без имен и без аргументов.
-
Применение функции — Черч использовал обозначение E 1 .E 2 для обозначения применения функции E 1 к фактическому аргументу E 2 . И все функции на один аргумент.
Создание функции — Черч ввел обозначение λx.E для обозначения функции, в которой «x» является формальным аргументом, а «E» — функциональным телом. Эти функции могут быть без имен и без аргументов.
Применение функции — Черч использовал обозначение E 1 .E 2 для обозначения применения функции E 1 к фактическому аргументу E 2 . И все функции на один аргумент.
Синтаксис лямбда-исчисления
Исчисление Ламдбы включает в себя три различных типа выражений:
E :: = x (переменные)
| E 1 E 2 (функция приложения)
| λx.E (создание функции)
Где λx.E называется лямбда-абстракцией, а E называется λ-выражением.
Оценка лямбда-исчисления
Чистое лямбда-исчисление не имеет встроенных функций. Давайте оценим следующее выражение —
(+ (* 5 6) (* 8 3))
Здесь мы не можем начать с «+», потому что он работает только с числами. Есть два приводимых выражения: (* 5 6) и (* 8 3).
Мы можем уменьшить либо один в первую очередь. Например —
(+ (* 5 6) (* 8 3)) (+ 30 (* 8 3)) (+ 30 24) = 54
β-редукция Правило
Нам нужно правило редукции для обработки λs
(λx . * 2 x) 4 (* 2 4) = 8
Это называется β-редукцией.
Формальный параметр может быть использован несколько раз —
(λx . + x x) 4 (+ 4 4) = 8
Когда есть несколько терминов, мы можем обработать их следующим образом:
(λx . (λx . + (− x 1)) x 3) 9
Внутренний x принадлежит внутреннему λ, а внешний x принадлежит внешнему.
(λx . + (− x 1)) 9 3 + (− 9 1) 3 + 8 3 = 11
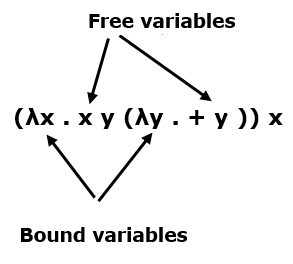
Свободные и связанные переменные
В выражении каждое появление переменной является либо «свободным» (для λ), либо «связанным» (для λ).
β-редукция (λx. E) y заменяет каждый x , свободный в E, на y . Например —
Альфа уменьшение
Альфа-сокращение очень просто, и это может быть сделано без изменения значения лямбда-выражения.
λx . (λx . x) (+ 1 x) ↔ α λx . (λy . y) (+ 1 x)
Например —
(λx . (λx . + (− x 1)) x 3) 9 (λx . (λy . + (− y 1)) x 3) 9 (λy . + (− y 1)) 9 3 + (− 9 1) 3 + 8 3 11
Теорема Черча-Россера
Теорема Черча-Россера гласит следующее:
Если E1 ↔ E2, то существует E, такое, что E1 → E и E2 → E. «Уменьшение любым способом может в конечном итоге привести к тому же результату».
Если E1 → E2, а E2 — нормальная форма, то происходит нормальное упорядочение E1 до E2. «Уменьшение нормального порядка всегда будет давать нормальную форму, если таковая существует».