Вы можете строить древовидные структуры данных из cons-ячеек, как списки списков.
Чтобы реализовать древовидные структуры, вам нужно спроектировать функциональные возможности, которые будут проходить через cons-ячейки в определенном порядке, например, предварительный порядок, порядок и порядок для двоичных деревьев.
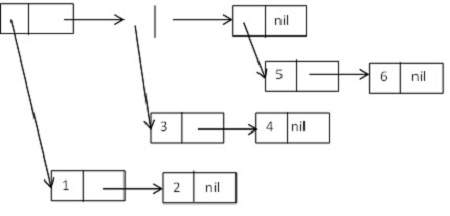
Дерево как список списков
Давайте рассмотрим древовидную структуру, состоящую из клеток cons, которые образуют следующий список списков:
((1 2) (3 4) (5 6)).
Схематически это можно выразить как —
Функции дерева в LISP
Хотя в основном вам нужно будет написать свои собственные древовидные функции в соответствии с вашими конкретными потребностями, LISP предоставляет некоторые древовидные функции, которые вы можете использовать.
Помимо всех функций списка, следующие функции работают особенно на древовидных структурах —
| Sr.No. | Описание функции |
|---|---|
| 1 |
дерево копий x & необязательный vecp Возвращает копию дерева cons клеток x. Он рекурсивно копирует как автомобиль, так и CDR. Если x не является cons-ячейкой, функция просто возвращает x без изменений. Если необязательный аргумент vecp равен true, эта функция копирует векторы (рекурсивно), а также cons-ячейки. |
| 2 |
равный дереву xy & key: test: test-not: key Он сравнивает два дерева минусов. Если x и y оба являются cons-ячейками, их машины и cdrs сравниваются рекурсивно. Если ни x, ни y не являются cons-ячейками, они сравниваются по eql или согласно указанному тесту. Функция: key, если указана, применяется к элементам обоих деревьев. |
| 3 |
sub новое старое дерево и ключ: test: test-not: key Он заменяет вхождения данного старого элемента новым элементом в дереве , которое является деревом клеток-противников. |
| 4 |
nsubst новое старое дерево и ключ: test: test-not: key Он работает так же, как и Sub, но уничтожает исходное дерево. |
| 5 |
Sublis Alist Tree & Key: тест: тест-не: ключ Он работает как субстрат, за исключением того, что он принимает список ассоциативных списков старых-новых пар. Каждый элемент дерева (после применения функции: key, если есть) сравнивается с машинами из alist; если он совпадает, он заменяется соответствующим CDR. |
| 6 |
nsublis alist tree & key: test: test-not: key Он работает так же, как Sublis, но деструктивная версия. |
дерево копий x & необязательный vecp
Возвращает копию дерева cons клеток x. Он рекурсивно копирует как автомобиль, так и CDR. Если x не является cons-ячейкой, функция просто возвращает x без изменений. Если необязательный аргумент vecp равен true, эта функция копирует векторы (рекурсивно), а также cons-ячейки.
равный дереву xy & key: test: test-not: key
Он сравнивает два дерева минусов. Если x и y оба являются cons-ячейками, их машины и cdrs сравниваются рекурсивно. Если ни x, ни y не являются cons-ячейками, они сравниваются по eql или согласно указанному тесту. Функция: key, если указана, применяется к элементам обоих деревьев.
sub новое старое дерево и ключ: test: test-not: key
Он заменяет вхождения данного старого элемента новым элементом в дереве , которое является деревом клеток-противников.
nsubst новое старое дерево и ключ: test: test-not: key
Он работает так же, как и Sub, но уничтожает исходное дерево.
Sublis Alist Tree & Key: тест: тест-не: ключ
Он работает как субстрат, за исключением того, что он принимает список ассоциативных списков старых-новых пар. Каждый элемент дерева (после применения функции: key, если есть) сравнивается с машинами из alist; если он совпадает, он заменяется соответствующим CDR.
nsublis alist tree & key: test: test-not: key
Он работает так же, как Sublis, но деструктивная версия.
Пример 1
Создайте новый файл исходного кода с именем main.lisp и введите в него следующий код.
(setq lst (list '(1 2) '(3 4) '(5 6))) (setq mylst (copy-list lst)) (setq tr (copy-tree lst)) (write lst) (terpri) (write mylst) (terpri) (write tr)
Когда вы выполняете код, он возвращает следующий результат —
((1 2) (3 4) (5 6)) ((1 2) (3 4) (5 6)) ((1 2) (3 4) (5 6))
Пример 2
Создайте новый файл исходного кода с именем main.lisp и введите в него следующий код.
(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9))))) (write tr) (setq trs (subst 7 1 tr)) (terpri) (write trs)
Когда вы выполняете код, он возвращает следующий результат —
((1 2 (3 4 5) ((7 8) (7 8 9)))) ((7 2 (3 4 5) ((7 8) (7 8 9))))
Строим свое дерево
Давайте попробуем построить наше собственное дерево, используя функции списка, доступные в LISP.
Сначала давайте создадим новый узел, который содержит некоторые данные
(defun make-tree (item) "it creates a new node with item." (cons (cons item nil) nil) )
Далее давайте добавим дочерний узел в дерево — он возьмет два узла дерева и добавит второе дерево в качестве дочернего для первого.
(defun add-child (tree child) (setf (car tree) (append (car tree) child)) tree)
Эта функция вернет первому дочернему элементу данное дерево — она возьмет узел дерева и вернет первого дочернего элемента этого узла, или nil, если у этого узла нет дочерних узлов.
(defun first-child (tree) (if (null tree) nil (cdr (car tree)) ) )
Эта функция будет возвращать следующего брата данного узла — она принимает узел дерева в качестве аргумента и возвращает ссылку на следующий узел брата, или nil, если у узла его нет.
(defun next-sibling (tree) (cdr tree) )
Наконец, нам нужна функция для возврата информации в узле —
(defun data (tree) (car (car tree)) )
пример
Этот пример использует вышеуказанные функции —
Создайте новый файл исходного кода с именем main.lisp и введите в него следующий код.
(defun make-tree (item) "it creates a new node with item." (cons (cons item nil) nil) ) (defun first-child (tree) (if (null tree) nil (cdr (car tree)) ) ) (defun next-sibling (tree) (cdr tree) ) (defun data (tree) (car (car tree)) ) (defun add-child (tree child) (setf (car tree) (append (car tree) child)) tree ) (setq tr '((1 2 (3 4 5) ((7 8) (7 8 9))))) (setq mytree (make-tree 10)) (write (data mytree)) (terpri) (write (first-child tr)) (terpri) (setq newtree (add-child tr mytree)) (terpri) (write newtree)
Когда вы выполняете код, он возвращает следующий результат —