Параллельный алгоритм — Введение

Алгоритм — это последовательность шагов, которые принимают входные данные от пользователя и после некоторых вычислений выдают выходные данные. Параллельный алгоритм — это алгоритм, который может выполнять несколько команд одновременно на разных устройствах обработки, а затем объединять все отдельные выходные данные для получения окончательного результата.

Параллельная обработка

Легкая доступность компьютеров наряду с ростом Интернета изменила способы хранения и обработки данных. Мы живем в эпоху, когда данные доступны в изобилии. Каждый день мы имеем дело с огромными объемами данных, которые требуют сложных вычислений, и это тоже, в короткие сроки. Иногда нам нужно извлекать данные из похожих или взаимосвязанных событий, которые происходят одновременно. Именно здесь нам требуется параллельная обработка, которая может разделить сложную задачу и обработать ее несколькими системами для быстрого вывода результатов.

Параллельная обработка необходима, когда задача заключается в обработке огромного объема сложных данных. Примеры включают в себя: доступ к большим базам данных, тестирование самолетов, астрономические расчеты, атомная и ядерная физика, биомедицинский анализ, экономическое планирование, обработка изображений, робототехника, прогнозирование погоды, веб-сервисы и т. Д.

Что такое параллелизм?

Параллелизм — это процесс обработки нескольких наборов инструкций одновременно. Это уменьшает общее время вычислений. Параллелизм может быть реализован с помощью параллельных компьютеров, то есть компьютеров со многими процессорами. Параллельные компьютеры требуют параллельного алгоритма, языков программирования, компиляторов и операционной системы, поддерживающей многозадачность.

В этом уроке мы обсудим только параллельные алгоритмы . Прежде чем двигаться дальше, давайте сначала поговорим об алгоритмах и их типах.

Что такое алгоритм?

Алгоритм — это последовательность инструкций для решения проблемы. При разработке алгоритма мы должны учитывать архитектуру компьютера, на котором будет выполняться алгоритм. Согласно архитектуре, существует два типа компьютеров —

• Последовательный компьютер
• Параллельный компьютер

В зависимости от архитектуры компьютеров, у нас есть два типа алгоритмов —

• Последовательный алгоритм — алгоритм, в котором некоторые последовательные шаги инструкций выполняются в хронологическом порядке для решения проблемы.

• Параллельный алгоритм . Задача делится на подзадачи и выполняется параллельно для получения отдельных выходных данных. Позже, эти отдельные выходы объединяются, чтобы получить конечный желаемый результат.

Последовательный алгоритм — алгоритм, в котором некоторые последовательные шаги инструкций выполняются в хронологическом порядке для решения проблемы.

Параллельный алгоритм . Задача делится на подзадачи и выполняется параллельно для получения отдельных выходных данных. Позже, эти отдельные выходы объединяются, чтобы получить конечный желаемый результат.

Нелегко разделить большую проблему на подзадачи . Подзадачи могут иметь зависимость данных между ними. Поэтому процессоры должны общаться друг с другом, чтобы решить проблему.

Было обнаружено, что время, необходимое процессорам для связи друг с другом, больше, чем фактическое время обработки. Таким образом, при разработке параллельного алгоритма необходимо учитывать правильную загрузку ЦП, чтобы получить эффективный алгоритм.

Чтобы правильно спроектировать алгоритм, мы должны иметь четкое представление об основной модели вычислений на параллельном компьютере.

Модель вычисления

Как последовательные, так и параллельные компьютеры работают с набором (потоком) инструкций, называемых алгоритмами. Этот набор инструкций (алгоритм) инструктирует компьютер о том, что он должен делать на каждом этапе.

В зависимости от потока команд и потока данных компьютеры можно разделить на четыре категории:

• Компьютеры с одним потоком команд, с одним потоком данных (SISD)
• Один поток инструкций, компьютеры с несколькими потоками данных (SIMD)
• Множественный поток команд, компьютеры с одним потоком данных (MISD)
• Компьютеры с несколькими потоками команд, несколькими потоками данных (MIMD)

SISD Компьютеры

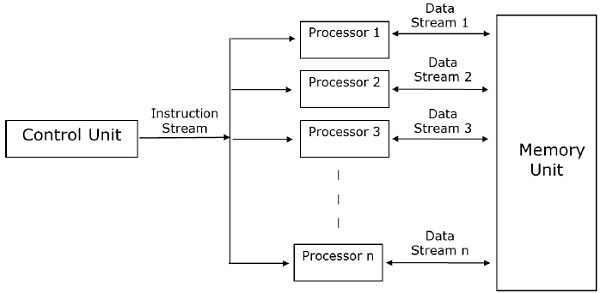
Компьютеры SISD содержат один блок управления, один блок обработки и один блок памяти .

В компьютерах этого типа процессор принимает единый поток инструкций от блока управления и работает с единым потоком данных из блока памяти. Во время вычислений на каждом этапе процессор принимает одну инструкцию от блока управления и оперирует единственными данными, полученными из блока памяти.

SIMD Компьютеры

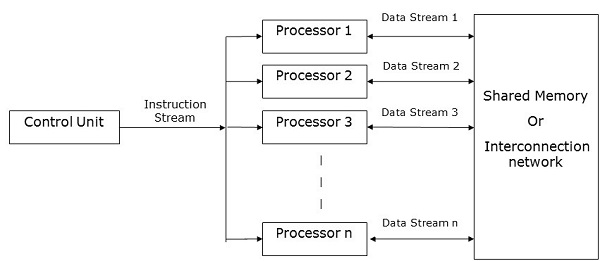
SIMD-компьютеры содержат один блок управления, несколько блоков обработки и общую память или сеть взаимосвязей .

Здесь один единственный блок управления отправляет инструкции всем процессорам. Во время вычислений на каждом шаге все процессоры получают единый набор инструкций от блока управления и работают с различным набором данных из блока памяти.

Каждый из блоков обработки имеет свой собственный локальный блок памяти для хранения как данных, так и инструкций. В компьютерах SIMD процессоры должны общаться между собой. Это делается общей памятью или сетью соединений .

В то время как некоторые из процессоров выполняют набор инструкций, остальные процессоры ждут своего следующего набора инструкций. Инструкции от блока управления решают, какой процессор будет активным (выполнять инструкции) или неактивным (дождаться следующей инструкции).

MISD Компьютеры

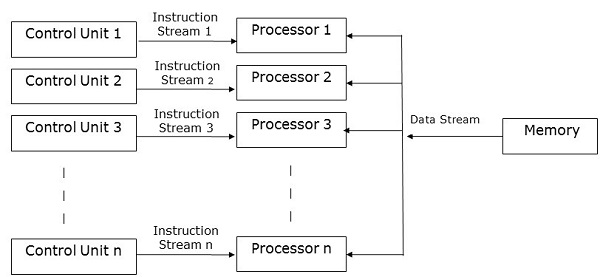
Как следует из названия, компьютеры MISD содержат несколько блоков управления, несколько блоков обработки и один общий блок памяти .

Здесь каждый процессор имеет свой собственный блок управления, и они имеют общий блок памяти. Все процессоры получают инструкции по отдельности от своего собственного блока управления, и они работают с одним потоком данных в соответствии с инструкциями, которые они получили от своих соответствующих блоков управления. Этот процессор работает одновременно.

MIMD Компьютеры

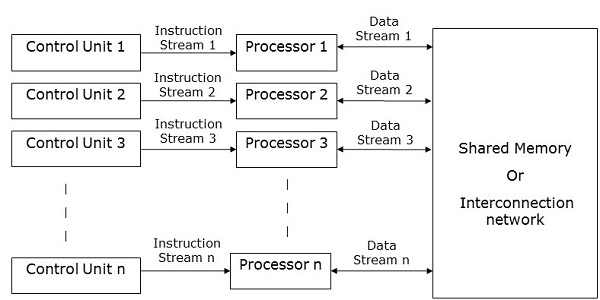
Компьютеры MIMD имеют несколько блоков управления, несколько блоков обработки и общую память или сеть взаимосвязей .

Здесь каждый процессор имеет свой собственный блок управления, локальный блок памяти и арифметико-логический блок. Они получают различные наборы инструкций от своих соответствующих блоков управления и работают с различными наборами данных.

Заметка

• Компьютер MIMD, который разделяет общую память, известен как мультипроцессоры, в то время как те, которые используют сеть взаимосвязи, известны как мультикомпьютеры .

• В зависимости от физического расстояния между процессорами мультикомпьютеры бывают двух типов:

  • Мультикомпьютер — когда все процессоры находятся очень близко друг к другу (например, в одной комнате).

  • Распределенная система — когда все процессоры находятся далеко друг от друга (например, в разных городах)

Компьютер MIMD, который разделяет общую память, известен как мультипроцессоры, в то время как те, которые используют сеть взаимосвязи, известны как мультикомпьютеры .

В зависимости от физического расстояния между процессорами мультикомпьютеры бывают двух типов:

Мультикомпьютер — когда все процессоры находятся очень близко друг к другу (например, в одной комнате).

Распределенная система — когда все процессоры находятся далеко друг от друга (например, в разных городах)

Параллельный алгоритм — анализ

Анализ алгоритма помогает нам определить, является ли алгоритм полезным или нет. Как правило, алгоритм анализируется на основе времени его выполнения (сложность времени) и количества пространства (сложность пространства), которое ему требуется.

Поскольку у нас есть сложные запоминающие устройства, доступные по разумной цене, пространство для хранения больше не является проблемой. Следовательно, космическая сложность не так важна.

Параллельные алгоритмы предназначены для повышения скорости вычислений на компьютере. Для анализа параллельного алгоритма мы обычно рассматриваем следующие параметры:

• Сложность времени (время выполнения),
• Общее количество используемых процессоров, и
• Общая стоимость.

Сложность времени

Основной причиной разработки параллельных алгоритмов было сокращение времени вычисления алгоритма. Таким образом, оценка времени выполнения алгоритма чрезвычайно важна при анализе его эффективности.

Время выполнения измеряется на основе времени, затраченного алгоритмом на решение проблемы. Общее время выполнения рассчитывается с момента начала выполнения алгоритма до момента его остановки. Если все процессоры не запускают или не завершают выполнение одновременно, то общее время выполнения алгоритма — это момент, когда первый процессор начал выполнение, до того момента, когда последний процессор прекратил выполнение.

Временную сложность алгоритма можно разделить на три категории:

• В худшем случае сложность — когда количество времени, необходимое алгоритму для данного ввода, максимально .

• Сложность среднего случая — когда количество времени, требуемое алгоритмом для заданного ввода, является средним .

• Сложность в лучшем случае — когда количество времени, необходимое алгоритму для заданного ввода, минимально .

В худшем случае сложность — когда количество времени, необходимое алгоритму для данного ввода, максимально .

Сложность среднего случая — когда количество времени, требуемое алгоритмом для заданного ввода, является средним .

Сложность в лучшем случае — когда количество времени, необходимое алгоритму для заданного ввода, минимально .

Асимптотический анализ

Сложность или эффективность алгоритма — это количество шагов, выполняемых алгоритмом для получения желаемого результата. Асимптотический анализ проводится для расчета сложности алгоритма при его теоретическом анализе. В асимптотическом анализе большая длина входных данных используется для вычисления функции сложности алгоритма.

Примечание. Асимптотика — это состояние, при котором прямая имеет тенденцию встречаться с кривой, но они не пересекаются. Здесь линия и кривая асимптотичны друг другу.

Асимптотическая запись — это самый простой способ описать самое быстрое и самое медленное время выполнения алгоритма с использованием высоких и низких ограничений по скорости. Для этого мы используем следующие обозначения —

• Обозначение Big O
• Обозначение омега
• Тэта нотация

Обозначение Big O

В математике обозначение Big O используется для представления асимптотических характеристик функций. Он представляет поведение функции для больших входных данных простым и точным методом. Это метод представления верхней границы времени выполнения алгоритма. Он представляет собой наибольшее количество времени, которое алгоритм может занять для завершения своего выполнения. Функция —

f (n) = O (g (n))

если существуют положительные постоянные c и n _0, такие что f (n) ≤ c * g (n) для всех n, где n ≥ n ₀ .

Обозначение омега

Нотация Omega — это метод представления нижней границы времени выполнения алгоритма. Функция —

f (n) = Ω (g (n))

если существуют положительные постоянные c и n _0, такие что f (n) ≥ c * g (n) для всех n, где n ≥ n ₀ .

Тэта нотация

Тета-нотация — это метод представления как нижней, так и верхней границы времени выполнения алгоритма. Функция —

f (n) = θ (g (n))

если существуют положительные постоянные c ₁ , c ₂ и n _0, такие что c1 * g (n) ≤ f (n) ≤ c2 * g (n) для всех n, где n ≥ n ₀ .

Ускорение алгоритма

Производительность параллельного алгоритма определяется путем расчета его ускорения . Ускорение определяется как отношение времени выполнения наихудшего случая самого быстрого известного последовательного алгоритма для конкретной задачи к времени наихудшего случая выполнения параллельного алгоритма.

Количество используемых процессоров

Количество используемых процессоров является важным фактором при анализе эффективности параллельного алгоритма. Стоимость покупки, обслуживания и запуска компьютеров рассчитывается. Чем больше число процессоров, используемых алгоритмом для решения задачи, тем дороже становится полученный результат.

Общая стоимость

Общая стоимость параллельного алгоритма является продуктом сложности времени и количества процессоров, используемых в этом конкретном алгоритме.

Общая стоимость = сложность времени × количество используемых процессоров

Следовательно, эффективность параллельного алгоритма составляет —

Параллельный алгоритм — Модели

Модель параллельного алгоритма разрабатывается путем рассмотрения стратегии разделения данных и метода обработки и применения подходящей стратегии для сокращения взаимодействий. В этой главе мы обсудим следующие модели параллельных алгоритмов:

• Параллельная модель данных
• Модель графа задач
• Модель рабочего бассейна
• Мастер раб модель
• Производитель потребитель или модель трубопровода
• Гибридная модель

Параллель данных

В параллельной модели данных задачи назначаются процессам, и каждая задача выполняет аналогичные типы операций с различными данными. Параллелизм данных является следствием отдельных операций, которые применяются к нескольким элементам данных.

Параллельная с данными модель может быть применена к общим адресным пространствам и парадигмам передачи сообщений. В модели, параллельной данным, накладные расходы на взаимодействие можно уменьшить, выбрав разложение, сохраняющее локальность, с помощью оптимизированных процедур коллективного взаимодействия или путем наложения вычислений и взаимодействия.

Основная характеристика проблем параллельной модели данных заключается в том, что интенсивность параллелизма данных увеличивается с увеличением размера проблемы, что, в свою очередь, позволяет использовать больше процессов для решения более крупных задач.

Пример — плотное матричное умножение.

Модель графа задач

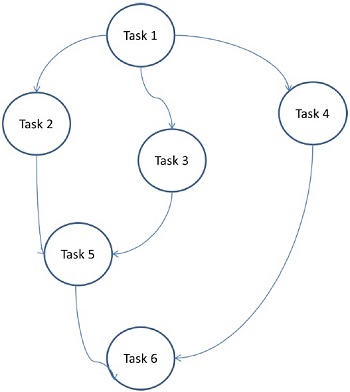
В модели графа задач параллелизм выражается графом задач . Граф задач может быть тривиальным или нетривиальным. В этой модели корреляция между задачами используется для продвижения местности или минимизации затрат на взаимодействие. Эта модель применяется для решения проблем, при которых количество данных, связанных с задачами, огромно по сравнению с количеством вычислений, связанных с ними. Задачи назначены, чтобы помочь улучшить стоимость перемещения данных между задачами.

Примеры — параллельная быстрая сортировка, разреженная матричная факторизация и параллельные алгоритмы, полученные с помощью подхода «разделяй и властвуй».

Здесь задачи делятся на элементарные задачи и реализуются в виде графика. Каждая задача — это независимая единица работы, которая зависит от одной или нескольких предыдущих задач. После завершения задачи выходные данные предыдущей задачи передаются зависимой задаче. Задача с предшествующей задачей начинает выполняться только после завершения всей предшествующей задачи. Окончательный вывод графика получается, когда завершается последняя зависимая задача (задача 6 на рисунке выше).

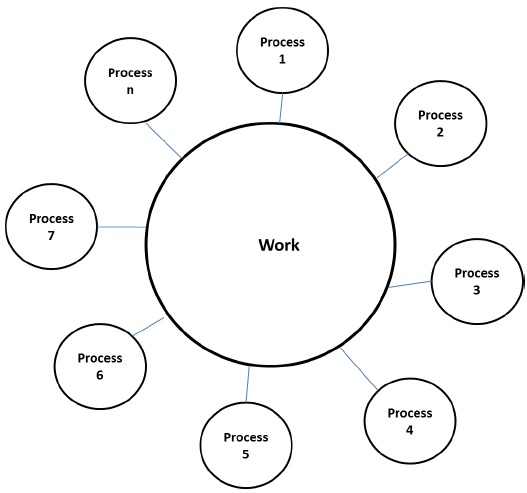
Модель рабочего бассейна

В модели рабочего пула задачи динамически назначаются процессам для балансировки нагрузки. Поэтому любой процесс может потенциально выполнить любую задачу. Эта модель используется, когда количество данных, связанных с задачами, сравнительно меньше, чем вычисление, связанное с задачами.

Нет желаемого предварительного назначения задач на процессы. Назначение задач является централизованным или децентрализованным. Указатели на задачи сохраняются в физически общем списке, в очереди приоритетов, или в хэш-таблице или дереве, или они могут быть сохранены в физически распределенной структуре данных.

Задача может быть доступна в начале или может быть сгенерирована динамически. Если задача генерируется динамически и выполняется децентрализованное назначение задачи, то требуется алгоритм обнаружения завершения, чтобы все процессы могли фактически обнаружить завершение всей программы и перестать искать другие задачи.

Пример — поиск параллельного дерева

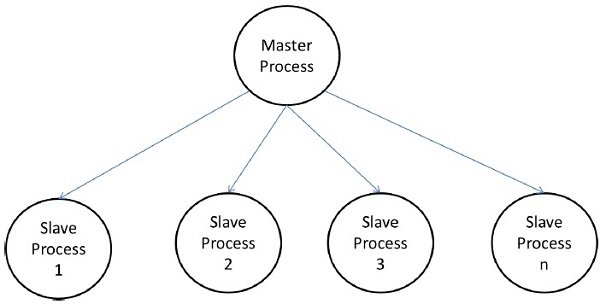
Мастер-Раб Модель

В модели «ведущий-ведомый» один или несколько мастер-процессов генерируют задачу и распределяют ее по подчиненным процессам. Задачи могут быть распределены заранее, если —

• мастер может оценить объем заданий, или
• случайное назначение может удовлетворительно справиться с балансировкой нагрузки, или
• рабам назначают меньшие части задачи в разное время.

Эта модель в целом одинаково подходит для парадигм общего адресного пространства или передачи сообщений, поскольку взаимодействие, естественно, происходит двумя способами.

В некоторых случаях задача может потребоваться выполнить поэтапно, и задача на каждом этапе должна быть завершена до того, как задача будет создана на следующих этапах. Модель «ведущий-ведомый» может быть обобщена на иерархическую или многоуровневую модель «ведущий-ведомый», в которой мастер верхнего уровня передает большую часть задач ведущему устройству второго уровня, который дополнительно подразделяет задачи между своими собственными ведомыми устройствами и может выполнять часть самой задачи.

Меры предосторожности при использовании модели «ведущий-ведомый»

Следует позаботиться о том, чтобы хозяин не стал точкой затора. Это может произойти, если задачи слишком малы или рабочие работают сравнительно быстро.

Задачи должны выбираться таким образом, чтобы стоимость выполнения задачи доминировала над стоимостью связи и стоимостью синхронизации.

Асинхронное взаимодействие может помочь перекрывать взаимодействие и вычисления, связанные с генерацией работы мастером.

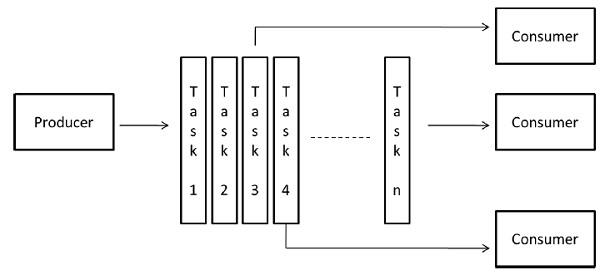
Модель трубопровода

Он также известен как модель производитель-потребитель . Здесь набор данных передается через серию процессов, каждый из которых выполняет определенную задачу. Здесь поступление новых данных генерирует выполнение новой задачи процессом в очереди. Процессы могут образовывать очередь в форме линейных или многомерных массивов, деревьев или общих графов с циклами или без них.

Эта модель представляет собой цепочку производителей и потребителей. Каждый процесс в очереди может рассматриваться как потребитель последовательности элементов данных для процесса, предшествующего ему в очереди, и как производитель данных для процесса, следующего за ним в очереди. Очередь не обязательно должна быть линейной цепочкой; это может быть ориентированный граф. Наиболее распространенным методом минимизации взаимодействия, применимым к этой модели, является перекрывающееся взаимодействие с вычислениями.

Пример — алгоритм параллельной LU-факторизации.

Гибридные модели

Гибридная модель алгоритма требуется, когда для решения проблемы может потребоваться более одной модели.

Гибридная модель может состоять из нескольких моделей, применяемых иерархически, или нескольких моделей, применяемых последовательно к различным фазам параллельного алгоритма.

Пример — параллельная быстрая сортировка

Параллельные машины с произвольным доступом

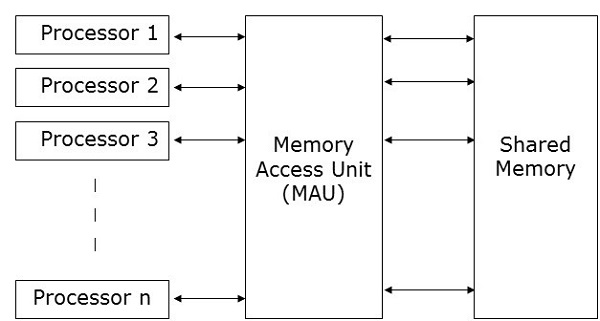
Параллельные машины произвольного доступа (PRAM) — это модель, которая рассматривается для большинства параллельных алгоритмов. Здесь несколько процессоров подключены к одному блоку памяти. Модель PRAM содержит —

• Набор процессоров аналогичного типа.

• Все процессоры имеют общий блок памяти. Процессоры могут общаться между собой только через общую память.

• Блок доступа к памяти (MAU) соединяет процессоры с одной общей памятью.

Набор процессоров аналогичного типа.

Все процессоры имеют общий блок памяти. Процессоры могут общаться между собой только через общую память.

Блок доступа к памяти (MAU) соединяет процессоры с одной общей памятью.

Здесь n числа процессоров могут выполнять независимые операции над n количеством данных в конкретную единицу времени. Это может привести к одновременному доступу к одной и той же ячейке памяти разными процессорами.

Для решения этой проблемы на модель PRAM были наложены следующие ограничения:

• Эксклюзивная чтение Эксклюзивная запись (EREW). Здесь нет двух процессоров, которые могут одновременно считывать или записывать данные в одну и ту же область памяти.

• Exclusive Read Concurrent Write (ERCW) — здесь двум процессорам не разрешено читать из одной и той же области памяти одновременно, но разрешено выполнять запись в одну и ту же область памяти одновременно.

• Одновременная запись с эксклюзивным чтением (CREW) — здесь всем процессорам разрешено выполнять чтение из одной и той же области памяти в одно и то же время, но не разрешено выполнять запись в одну и ту же область памяти в одно и то же время.

• Одновременное чтение Одновременная запись (CRCW) — всем процессорам разрешено выполнять чтение или запись в одну и ту же ячейку памяти одновременно.

Эксклюзивная чтение Эксклюзивная запись (EREW). Здесь нет двух процессоров, которые могут одновременно считывать или записывать данные в одну и ту же область памяти.

Exclusive Read Concurrent Write (ERCW) — здесь двум процессорам не разрешено читать из одной и той же области памяти одновременно, но разрешено выполнять запись в одну и ту же область памяти одновременно.

Одновременная запись с эксклюзивным чтением (CREW) — здесь всем процессорам разрешено выполнять чтение из одной и той же области памяти в одно и то же время, но не разрешено выполнять запись в одну и ту же область памяти в одно и то же время.

Одновременное чтение Одновременная запись (CRCW) — всем процессорам разрешено выполнять чтение или запись в одну и ту же ячейку памяти одновременно.

Существует много методов для реализации модели PRAM, но наиболее выдающимися являются:

• Модель с общей памятью
• Модель передачи сообщений
• Параллельная модель данных

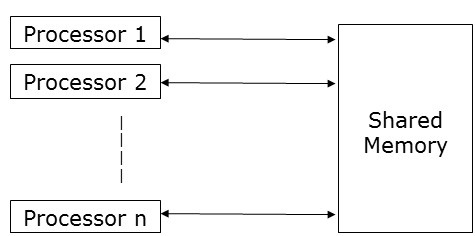
Модель общей памяти

Общая память делает упор на параллелизм управления, а не на параллелизм данных . В модели с общей памятью несколько процессов выполняются на разных процессорах независимо, но они совместно используют общее пространство памяти. Из-за какой-либо активности процессора, если есть какое-либо изменение в какой-либо области памяти, это видно остальным процессорам.

Поскольку несколько процессоров обращаются к одной и той же ячейке памяти, может случиться так, что в любой конкретный момент времени более одного процессора обращаются к одной и той же ячейке памяти. Предположим, что один читает это местоположение, а другой пишет в этом месте. Это может создать путаницу. Чтобы избежать этого, для обеспечения взаимного исключения реализован некоторый механизм управления, такой как блокировка / семафор .

Программирование общей памяти было реализовано следующим образом:

• Библиотеки потоков. Библиотека потоков позволяет нескольким элементам управления одновременно работать в одной и той же области памяти. Библиотека потоков предоставляет интерфейс, который поддерживает многопоточность через библиотеку подпрограмм. Содержит подпрограммы для

  • Создание и уничтожение потоков
  • Планирование выполнения потока
  • передача данных и сообщений между потоками
  • сохранение и восстановление контекстов потока

Библиотеки потоков. Библиотека потоков позволяет нескольким элементам управления одновременно работать в одной и той же области памяти. Библиотека потоков предоставляет интерфейс, который поддерживает многопоточность через библиотеку подпрограмм. Содержит подпрограммы для

Примеры библиотек потоков: потоки SolarisTM для Solaris, потоки POSIX, реализованные в Linux, потоки Win32, доступные в Windows NT и Windows 2000, и потоки JavaTM как часть стандартного комплекта разработки JavaTM (JDK).

• Системы с распределенной общей памятью (DSM) — системы DSM создают абстракцию совместно используемой памяти в слабо связанной архитектуре для реализации программирования совместно используемой памяти без аппаратной поддержки. Они реализуют стандартные библиотеки и используют расширенные функции управления памятью на уровне пользователя, имеющиеся в современных операционных системах. Примерами являются система протекторов, Munin, IVY, Shasta, Brazos и Cashmere.

• Пакеты аннотаций программы — это реализовано на архитектурах, имеющих одинаковые характеристики доступа к памяти. Наиболее ярким примером пакетов аннотаций программ является OpenMP. OpenMP реализует функциональный параллелизм. Основное внимание уделяется распараллеливанию циклов.

Системы с распределенной общей памятью (DSM) — системы DSM создают абстракцию совместно используемой памяти в слабо связанной архитектуре для реализации программирования совместно используемой памяти без аппаратной поддержки. Они реализуют стандартные библиотеки и используют расширенные функции управления памятью на уровне пользователя, имеющиеся в современных операционных системах. Примерами являются система протекторов, Munin, IVY, Shasta, Brazos и Cashmere.

Пакеты аннотаций программы — это реализовано на архитектурах, имеющих одинаковые характеристики доступа к памяти. Наиболее ярким примером пакетов аннотаций программ является OpenMP. OpenMP реализует функциональный параллелизм. Основное внимание уделяется распараллеливанию циклов.

Концепция разделяемой памяти обеспечивает низкоуровневое управление системой разделяемой памяти, но, как правило, она утомительна и ошибочна. Это более применимо для системного программирования, чем прикладное программирование.

Преимущества совместного использования памяти

• Глобальное адресное пространство дает удобный для пользователя подход к программированию памяти.

• Благодаря близости памяти к процессору, обмен данными между процессами происходит быстро и равномерно.

• Нет необходимости четко определять передачу данных между процессами.

• Затраты на процесс-коммуникацию незначительны.

• Это очень легко учиться.

Глобальное адресное пространство дает удобный для пользователя подход к программированию памяти.

Благодаря близости памяти к процессору, обмен данными между процессами происходит быстро и равномерно.

Нет необходимости четко определять передачу данных между процессами.

Затраты на процесс-коммуникацию незначительны.

Это очень легко учиться.

Недостатки совместного использования памяти

• Это не портативный.
• Управление локальностью данных очень сложно.

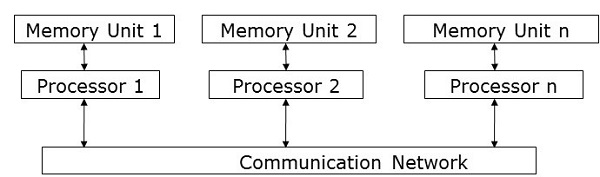
Модель передачи сообщений

Передача сообщений является наиболее часто используемым подходом параллельного программирования в системах с распределенной памятью. Здесь программист должен определить параллелизм. В этой модели все процессоры имеют свой собственный локальный блок памяти и обмениваются данными через сеть связи.

Процессоры используют библиотеки передачи сообщений для связи между собой. Помимо отправляемых данных, сообщение содержит следующие компоненты:

• Адрес процессора, с которого отправляется сообщение;

• Начальный адрес ячейки памяти данных в отправляющем процессоре;

• Тип данных отправляемых данных;

• Размер данных отправляемых данных;

• Адрес процессора, на который отправляется сообщение;

• Начальный адрес ячейки памяти для данных в принимающем процессоре.

Адрес процессора, с которого отправляется сообщение;

Начальный адрес ячейки памяти данных в отправляющем процессоре;

Тип данных отправляемых данных;

Размер данных отправляемых данных;

Адрес процессора, на который отправляется сообщение;

Начальный адрес ячейки памяти для данных в принимающем процессоре.

Процессоры могут общаться друг с другом любым из следующих способов:

• Двухточечная связь
• Коллективное общение
• Интерфейс передачи сообщений

Двухточечная связь

Двухточечная связь — это самая простая форма передачи сообщений. Здесь сообщение может быть отправлено с отправляющего процессора на принимающий процессор с помощью любого из следующих режимов передачи:

• Синхронный режим — следующее сообщение отправляется только после получения подтверждения того, что его предыдущее сообщение было доставлено, для поддержания последовательности сообщения.

• Асинхронный режим — для отправки следующего сообщения получение подтверждения доставки предыдущего сообщения не требуется.

Синхронный режим — следующее сообщение отправляется только после получения подтверждения того, что его предыдущее сообщение было доставлено, для поддержания последовательности сообщения.

Асинхронный режим — для отправки следующего сообщения получение подтверждения доставки предыдущего сообщения не требуется.

Коллективное общение

Коллективное общение включает в себя более двух процессоров для передачи сообщений. Следующие режимы позволяют коллективные коммуникации —

• Барьер — Барьерный режим возможен, если все процессоры, включенные в коммуникацию, запускают определенный блок (известный как барьерный блок ) для передачи сообщений.

• Вещание — Вещание бывает двух типов —

  • One-to-all — Здесь один процессор с одной операцией отправляет одно и то же сообщение всем другим процессорам.

  • All-to-all — Здесь все процессоры отправляют сообщения всем остальным процессорам.

Барьер — Барьерный режим возможен, если все процессоры, включенные в коммуникацию, запускают определенный блок (известный как барьерный блок ) для передачи сообщений.

Вещание — Вещание бывает двух типов —

One-to-all — Здесь один процессор с одной операцией отправляет одно и то же сообщение всем другим процессорам.

All-to-all — Здесь все процессоры отправляют сообщения всем остальным процессорам.

Передаваемые сообщения могут быть трех типов:

• Персонализированные — уникальные сообщения отправляются всем другим процессорам назначения.

• Неперсонализированный — все процессоры назначения получают одно и то же сообщение.

• Сокращение — при сокращенном широковещании один процессор группы собирает все сообщения от всех других процессоров в группе и объединяет их в одно сообщение, к которому могут обращаться все остальные процессоры в группе.

Персонализированные — уникальные сообщения отправляются всем другим процессорам назначения.

Неперсонализированный — все процессоры назначения получают одно и то же сообщение.

Сокращение — при сокращенном широковещании один процессор группы собирает все сообщения от всех других процессоров в группе и объединяет их в одно сообщение, к которому могут обращаться все остальные процессоры в группе.

Преимущества передачи сообщений

• Обеспечивает низкоуровневое управление параллелизмом;
• Это портативный;
• Меньше ошибок;
• Меньше накладных расходов при параллельной синхронизации и распределении данных.

Недостатки передачи сообщений

• По сравнению с параллельным кодом совместно используемой памяти для кода передачи сообщений обычно требуется больше программных издержек.

По сравнению с параллельным кодом совместно используемой памяти для кода передачи сообщений обычно требуется больше программных издержек.

Библиотеки передачи сообщений

Есть много библиотек для передачи сообщений. Здесь мы обсудим две наиболее часто используемые библиотеки для передачи сообщений —

• Интерфейс передачи сообщений (MPI)
• Параллельная виртуальная машина (PVM)

Интерфейс передачи сообщений (MPI)

Это универсальный стандарт для обеспечения связи между всеми параллельными процессами в системе распределенной памяти. Большинство обычно используемых параллельных вычислительных платформ обеспечивают по крайней мере одну реализацию интерфейса передачи сообщений. Он был реализован как набор предопределенных функций, называемых библиотекой, и может вызываться из таких языков, как C, C ++, Fortran и т. Д. MPI являются быстрыми и переносимыми по сравнению с другими библиотеками передачи сообщений.

Преимущества интерфейса передачи сообщений

• Работает только на архитектурах с общей памятью или архитектурах с распределенной памятью;

• Каждый процессор имеет свои локальные переменные;

• По сравнению с большими компьютерами с общей памятью компьютеры с распределенной памятью дешевле.

Работает только на архитектурах с общей памятью или архитектурах с распределенной памятью;

Каждый процессор имеет свои локальные переменные;

По сравнению с большими компьютерами с общей памятью компьютеры с распределенной памятью дешевле.

Недостатки интерфейса передачи сообщений

• Для параллельного алгоритма требуется больше программных изменений;
• Иногда трудно отладить; а также
• Не работает хорошо в сети связи между узлами.

Параллельная виртуальная машина (PVM)

PVM — это портативная система передачи сообщений, предназначенная для соединения отдельных разнородных хост-машин в единую виртуальную машину. Это единый управляемый ресурс параллельных вычислений. Большие вычислительные проблемы, такие как исследования сверхпроводимости, моделирование молекулярной динамики и матричные алгоритмы, могут быть решены более экономически эффективно с использованием памяти и совокупной мощности многих компьютеров. Он управляет всеми маршрутизацией сообщений, преобразованием данных, планированием задач в сети несовместимых компьютерных архитектур.

Особенности PVM

• Очень прост в установке и настройке;
• Несколько пользователей могут использовать PVM одновременно;
• Один пользователь может выполнять несколько приложений;
• Это небольшой пакет;
• Поддерживает C, C ++, Fortran;
• Для данного запуска программы PVM пользователи могут выбрать группу машин;
• Это модель передачи сообщений,
• Процессные вычисления;
• Поддерживает гетерогенную архитектуру.

Параллельное программирование данных

Основное внимание в модели параллельного программирования данных уделяется одновременному выполнению операций над набором данных. Набор данных организован в некоторую структуру, такую ​​как массив, гиперкуб и т. Д. Процессоры совместно выполняют операции над одной и той же структурой данных. Каждая задача выполняется в отдельном разделе с одинаковой структурой данных.

Это ограничение, так как не все алгоритмы могут быть определены с точки зрения параллелизма данных. Это причина, почему параллелизм данных не является универсальным.

Языки параллельных данных помогают определить декомпозицию и отображение данных на процессоры. Он также включает в себя операторы распределения данных, которые позволяют программисту контролировать данные — например, какие данные будут поступать на какой процессор — чтобы уменьшить объем связи внутри процессоров.

Параллельный алгоритм — структура

Чтобы правильно применить любой алгоритм, очень важно выбрать правильную структуру данных. Это связано с тем, что конкретная операция, выполняемая над структурой данных, может занять больше времени по сравнению с той же операцией, выполняемой над другой структурой данных.

Пример. Для доступа к i- ^му элементу в наборе с использованием массива может потребоваться постоянное время, но при использовании связанного списка время, необходимое для выполнения той же операции, может стать полиномом.

Следовательно, выбор структуры данных должен выполняться с учетом архитектуры и типа выполняемых операций.

Следующие структуры данных обычно используются в параллельном программировании —

• Связанный список
• Массивы
• Сеть гиперкубов

Связанный список

Связанный список — это структура данных, имеющая ноль или более узлов, связанных указателями. Узлы могут занимать или не занимать последовательные области памяти. Каждый узел состоит из двух или трех частей — одна часть данных, в которой хранятся данные, а две другие — это поля ссылок , в которых хранится адрес предыдущего или следующего узла. Адрес первого узла хранится во внешнем указателе, называемом головой . Последний узел, известный как tail, обычно не содержит никакого адреса.

Есть три типа связанных списков —

• Единственный связанный список
• Двусвязный список
• Круговой связанный список

Единственный связанный список

Узел односвязного списка содержит данные и адрес следующего узла. Внешний указатель с именем head хранит адрес первого узла.

Двусвязный список

Узел двусвязного списка содержит данные и адрес как предыдущего, так и следующего узла. Внешний указатель с именем head хранит адрес первого узла, а внешний указатель с именем tail хранит адрес последнего узла.

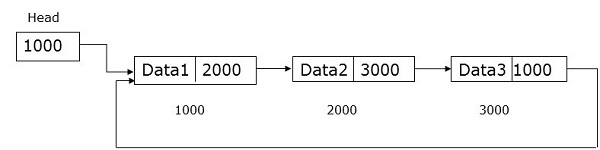
Круговой связанный список

Круговой связанный список очень похож на односвязный список за исключением того факта, что последний узел сохранил адрес первого узла.

Массивы

Массив — это структура данных, в которой мы можем хранить похожие типы данных. Это может быть одномерный или многомерный. Массивы могут быть созданы статически или динамически.

• В статически объявленных массивах размер и размер массивов известны во время компиляции.

• В динамически объявленных массивах размер и размер массива известны во время выполнения.

В статически объявленных массивах размер и размер массивов известны во время компиляции.

В динамически объявленных массивах размер и размер массива известны во время выполнения.

При программировании с общей памятью массивы можно использовать как общую память, а при параллельном программировании данных их можно использовать путем разбиения на подмассивы.

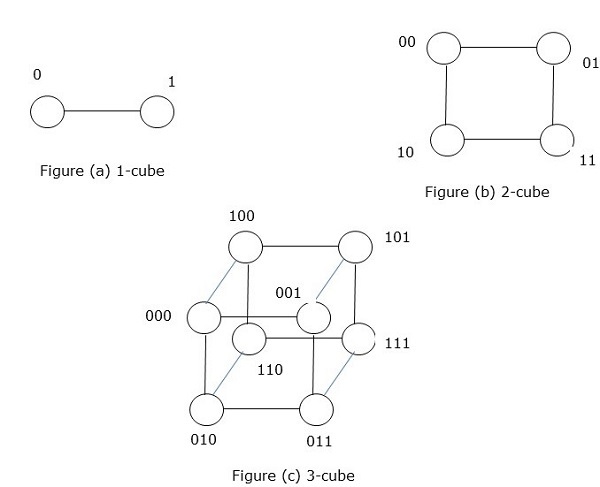
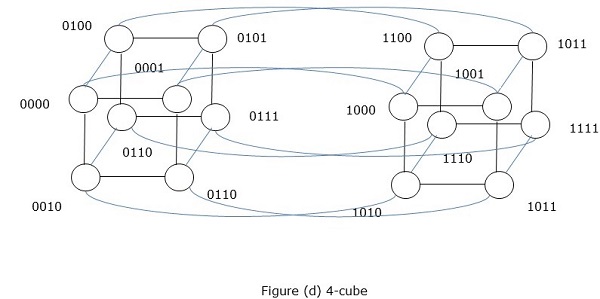
Сеть гиперкубов

Архитектура гиперкуба полезна для тех параллельных алгоритмов, где каждая задача должна взаимодействовать с другими задачами. Топология гиперкуба может легко встраивать другие топологии, такие как кольцо и сетка. Это также известно как n-кубов, где n — число измерений. Гиперкуб может быть построен рекурсивно.

Параллельный алгоритм — методы проектирования

Выбор правильной методики проектирования для параллельного алгоритма является наиболее сложной и важной задачей. Большинство проблем параллельного программирования может иметь более одного решения. В этой главе мы обсудим следующие методы проектирования параллельных алгоритмов:

• Разделяй и властвуй
• Жадный метод
• Динамическое программирование
• Откат
• Филиал & Связанный
• Линейное программирование

Метод разделяй и властвуй

В подходе «разделяй и властвуй» проблема делится на несколько небольших подзадач. Затем подзадачи решаются рекурсивно и объединяются, чтобы получить решение исходной задачи.

Подход «разделяй и властвуй» включает в себя следующие шаги на каждом уровне —

• Разделить — исходная проблема делится на подзадачи.

• Завоевать — Подзадачи решаются рекурсивно.

• Объединить — Решения подзадач объединяются, чтобы получить решение исходной проблемы.

Разделить — исходная проблема делится на подзадачи.

Завоевать — Подзадачи решаются рекурсивно.

Объединить — Решения подзадач объединяются, чтобы получить решение исходной проблемы.

Подход «разделяй и властвуй» применяется в следующих алгоритмах:

• Бинарный поиск
• Быстрая сортировка
• Сортировка слиянием
• Целочисленное умножение
• Матричная инверсия
• Матричное умножение

Жадный метод

В жадном алгоритме оптимизации решения наилучшее решение выбирается в любой момент. Жадный алгоритм очень легко применить к сложным задачам. Он решает, какой шаг обеспечит наиболее точное решение на следующем шаге.

Этот алгоритм называется жадным, потому что когда предоставляется оптимальное решение для меньшего экземпляра, алгоритм не учитывает всю программу в целом. Как только решение рассматривается, жадный алгоритм никогда не рассматривает то же самое решение снова.

Жадный алгоритм работает рекурсивно, создавая группу объектов из наименьших возможных составных частей. Рекурсия — это процедура для решения проблемы, в которой решение конкретной проблемы зависит от решения меньшего экземпляра этой проблемы.

Динамическое программирование

Динамическое программирование — это метод оптимизации, который делит проблему на более мелкие подзадачи, и после решения каждой подзадачи динамическое программирование объединяет все решения, чтобы получить окончательное решение. В отличие от метода «разделяй и властвуй», динамическое программирование многократно использует решение подзадач.

Рекурсивный алгоритм для рядов Фибоначчи является примером динамического программирования.

Алгоритм возврата

Backtracking — это метод оптимизации для решения комбинационных задач. Он применяется как для программных, так и для реальных задач. Проблема восьмерки, головоломка судоку и прохождение лабиринта — популярные примеры использования алгоритма возврата.

В обратном порядке мы начнем с возможного решения, которое удовлетворяет всем необходимым условиям. Затем мы переходим на следующий уровень и, если этот уровень не дает удовлетворительного решения, мы возвращаемся на один уровень назад и начинаем с новой опции.

Ветвь и Связка

Алгоритм ветвления и ограничения — это метод оптимизации, позволяющий получить оптимальное решение проблемы. Он ищет лучшее решение для данной проблемы во всем пространстве решения. Границы оптимизируемой функции объединяются со значением самого последнего лучшего решения. Это позволяет алгоритму полностью находить части пространства решений.

Цель поиска по ветвям и привязкам — поддерживать путь к цели с наименьшими затратами. Как только решение найдено, оно может продолжать улучшать решение. Поиск ветвей и границ реализован в поиске с ограничением по глубине и поиском по глубине.

Линейное программирование

Линейное программирование описывает широкий класс задач оптимизации, где и критерий оптимизации, и ограничения являются линейными функциями. Это метод получения наилучшего результата, например, максимальной прибыли, кратчайшего пути или минимальной стоимости.

В этом программировании у нас есть набор переменных, и мы должны присваивать им абсолютные значения, чтобы удовлетворить набор линейных уравнений и максимизировать или минимизировать заданную линейную целевую функцию.

Параллельный алгоритм — умножение матриц

Матрица — это набор числовых и нечисловых данных, расположенных в фиксированном количестве строк и столбцов. Матричное умножение является важным проектом умножения в параллельных вычислениях. Здесь мы обсудим реализацию умножения матриц в различных сетях связи, таких как меш и гиперкуб. Сетка и гиперкуб имеют более высокое сетевое соединение, поэтому они обеспечивают более быстрый алгоритм, чем другие сети, такие как кольцевая сеть.

Сетчатая сеть

Топология, в которой набор узлов образует p-мерную сетку, называется сеточной топологией. Здесь все ребра параллельны оси сетки, и все соседние узлы могут связываться между собой.

Общее количество узлов = (количество узлов в строке) × (количество узлов в столбце)

Ячеистая сеть может быть оценена с использованием следующих факторов:

• Диаметр
• Ширина деления пополам

Диаметр — в ячеистой сети самое большое расстояние между двумя узлами — это его диаметр. P-мерная ячеистая сеть, имеющая kP узлы, имеет диаметр p (k – 1) .

Ширина деления пополам — ширина деления пополам — это минимальное количество ребер, которые необходимо удалить из сети, чтобы разделить сеть ячеек на две половины.

Умножение матриц с использованием ячеистой сети

Мы рассмотрели модель SIMD 2D ячеистой сети, имеющую циклические соединения. Мы разработаем алгоритм для умножения двух n × n массивов с использованием n ² процессоров за определенный промежуток времени.

Матрицы A и B имеют элементы a _ij и b _ij соответственно. Элемент обработки PE _ij представляет собой _ij и b _ij . Расположите матрицы A и B таким образом, чтобы у каждого процессора была пара умножаемых элементов. Элементы матрицы A будут двигаться в левом направлении, а элементы матрицы B — в направлении вверх. Эти изменения в положении элементов в матрицах A и B представляют каждому элементу обработки PE новую пару значений для умножения.

Шаги в алгоритме

• Потрясите две матрицы.
• Рассчитать все произведения, а _ik × b _kj
• Подсчитайте суммы, когда шаг 2 завершен.

Алгоритм

Procedure MatrixMulti

Begin
   for k = 1 to n-1
	
   for all Pij; where i and j ranges from 1 to n
      ifi is greater than k then
         rotate a in left direction
      end if
		
   if j is greater than k then
      rotate b in the upward direction
   end if
	
   for all Pij ; where i and j lies between 1 and n
      compute the product of a and b and store it in c
   for k= 1 to n-1 step 1
   for all Pi;j where i and j ranges from 1 to n
      rotate a in left direction
      rotate b in the upward direction
      c=c+aXb
End

Сеть гиперкубов

Гиперкуб — это n-мерная конструкция, в которой ребра перпендикулярны между собой и имеют одинаковую длину. N-мерный гиперкуб также известен как n-куб или n-мерный куб.

Особенности гиперкуба с узлом 2 ^k

• Диаметр = к
• Ширина деления пополам = 2 ^{к – 1}
• Количество ребер = k

Умножение матриц с использованием сети HyperCube

Общая спецификация сетей Гиперкуб —

• Пусть N = 2 ^m будет общим числом процессоров. Пусть процессоры будут P _0, P ₁ … ..P _N-1 .

• Пусть i и i ^b — два целых числа, 0 <i, i ^b <N-1, и его двоичное представление отличается только положением b, 0 <b <k – 1.

• Рассмотрим две матрицы n × n, матрицу A и матрицу B.

• Шаг 1 — Элементы матрицы A и матрицы B назначены n ³ процессорам, так что процессор в позиции i, j, k будет иметь _ji и b _ik .

• Шаг 2 — Весь процессор в позиции (i, j, k) вычисляет произведение

  C (i, j, k) = A (i, j, k) × B (i, j, k)

• Шаг 3 — Сумма C (0, j, k) = ΣC (i, j, k) для 0 ≤ i ≤ n-1, где 0 ≤ j, k <n – 1.

Пусть N = 2 ^m будет общим числом процессоров. Пусть процессоры будут P _0, P ₁ … ..P _N-1 .

Пусть i и i ^b — два целых числа, 0 <i, i ^b <N-1, и его двоичное представление отличается только положением b, 0 <b <k – 1.

Рассмотрим две матрицы n × n, матрицу A и матрицу B.

Шаг 1 — Элементы матрицы A и матрицы B назначены n ³ процессорам, так что процессор в позиции i, j, k будет иметь _ji и b _ik .

Шаг 2 — Весь процессор в позиции (i, j, k) вычисляет произведение

C (i, j, k) = A (i, j, k) × B (i, j, k)

Шаг 3 — Сумма C (0, j, k) = ΣC (i, j, k) для 0 ≤ i ≤ n-1, где 0 ≤ j, k <n – 1.

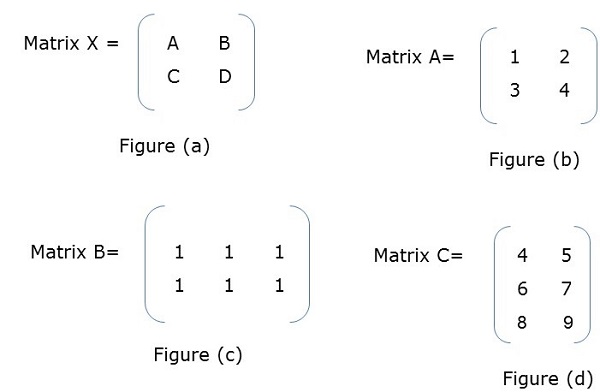
Блочная матрица

Блочная матрица или секционированная матрица — это матрица, в которой каждый элемент сам представляет отдельную матрицу. Эти отдельные секции известны как блок или субматрица .

пример

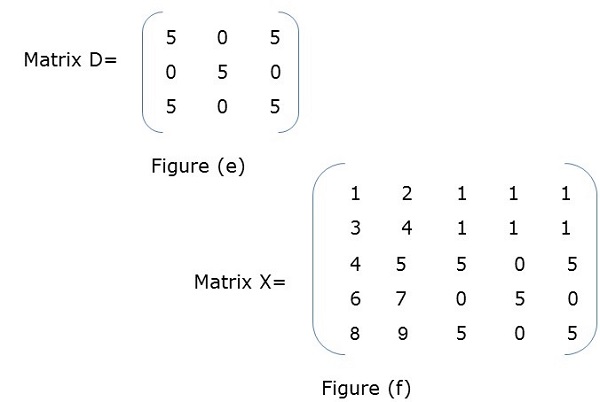
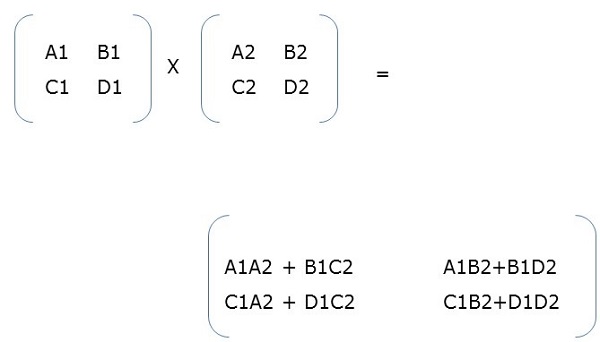
На рисунке (а) X представляет собой блочную матрицу, где A, B, C, D сами являются матрицами. Рисунок (f) показывает общую матрицу.

Блочное матричное умножение

Когда две блочные матрицы являются квадратными матрицами, они умножаются так же, как мы выполняем простое умножение матриц. Например,

Параллельный алгоритм — сортировка

Сортировка — это процесс расположения элементов в группе в определенном порядке, то есть в порядке возрастания, в порядке убывания, в алфавитном порядке и т. Д. Здесь мы обсудим следующее:

• Перечень сортировки
• Нечетно-четное транспонирование
• Параллельная сортировка слиянием
• Hyper Quick Sort

Сортировка списка элементов — очень распространенная операция. Алгоритм последовательной сортировки может быть недостаточно эффективным, когда нам приходится сортировать огромный объем данных. Поэтому в сортировке используются параллельные алгоритмы.

Перечень сортировки

Сортировка перечисления — это способ упорядочения всех элементов в списке путем нахождения конечной позиции каждого элемента в отсортированном списке. Это делается путем сравнения каждого элемента со всеми другими элементами и определения количества элементов, имеющих меньшее значение.

Следовательно, для любых двух элементов a _i и a _j любой из следующих случаев должен быть истинным:

• а _я <а _ж
• а _я > а _ж
• a _i = a _j

Алгоритм

procedure ENUM_SORTING (n)

begin
   for each process P 1,j do
      C[j] := 0;
		
   for each process P i, j do
	
      if (A[i] < A[j]) or A[i] = A[j] and i < j) then
         C[j] := 1;
      else
         C[j] := 0;
			
   for each process P1, j do
      A[C[j]] := A[j];
		
end ENUM_SORTING

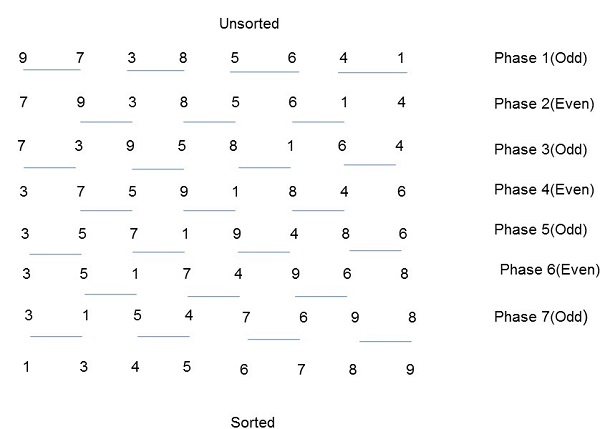
Нечетно-четное транспонирование

Нечетно-четная транспонированная сортировка основана на методе Bubble Sort. Он сравнивает два соседних числа и переключает их, если первое число больше второго, чтобы получить список в порядке возрастания. Противоположный случай применяется для ряда в порядке убывания. Нечетно-четная транспонированная сортировка работает в двух фазах — нечетной и четной фазах . На обоих этапах процессы обмениваются номерами со смежными номерами справа.

Алгоритм

procedure ODD-EVEN_PAR (n) 

begin 
   id := process's label 
	
   for i := 1 to n do 
   begin 
	
      if i is odd and id is odd then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
      if i is even and id is even then 
         compare-exchange_min(id + 1); 
      else 
         compare-exchange_max(id - 1);
			
   end for
	
end ODD-EVEN_PAR

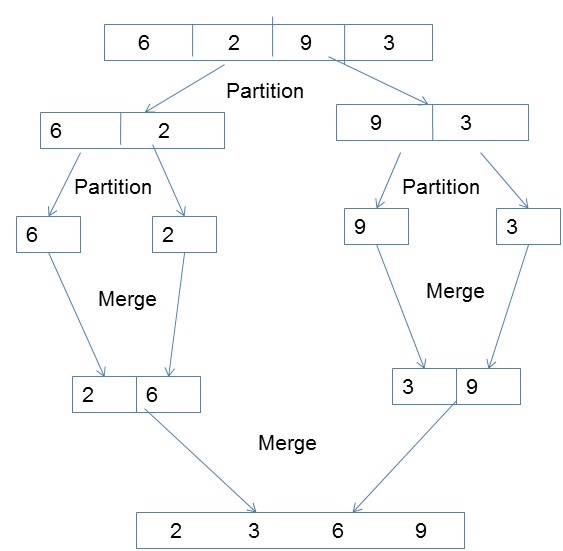
Параллельная сортировка слиянием

Сортировка слиянием сначала делит несортированный список на наименьшие возможные подсписки, сравнивает его со смежным списком и объединяет его в отсортированном порядке. Он очень хорошо реализует параллелизм, следуя алгоритму «разделяй и властвуй».

Алгоритм

procedureparallelmergesort(id, n, data, newdata)

begin
   data = sequentialmergesort(data)
	
      for dim = 1 to n
         data = parallelmerge(id, dim, data)
      endfor
		
   newdata = data
end

Hyper Quick Sort

Hyper quick sort — это реализация быстрой сортировки на гиперкубе. Его шаги следующие:

• Разделите несортированный список по каждому узлу.
• Сортировка каждого узла локально.
• Из узла 0 передайте медианное значение.
• Разделите каждый список локально, а затем обменяйтесь половинами по верхнему измерению.
• Повторите шаги 3 и 4 параллельно, пока размер не достигнет 0.

Алгоритм

procedure HYPERQUICKSORT (B, n)
begin

   id := process’s label;
	
   for i := 1 to d do
      begin
      x := pivot;
      partition B into B1 and B2 such that B1 ≤ x < B2;
      if ith bit is 0 then
		
      begin
         send B2 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B1 U C;
      endif
      
      else
         send B1 to the process along the ith communication link;
         C := subsequence received along the ith communication link;
         B := B2 U C;
         end else
      end for
		
   sort B using sequential quicksort;
	
end HYPERQUICKSORT

Алгоритм параллельного поиска

Поиск является одной из фундаментальных операций в информатике. Он используется во всех приложениях, где нам нужно найти, находится ли элемент в данном списке или нет. В этой главе мы обсудим следующие алгоритмы поиска —

• Разделяй и властвуй
• Поиск в глубину
• Поиск в ширину
• Best-First Search

Разделяй и властвуй

При подходе «разделяй и властвуй» проблема делится на несколько небольших подзадач. Затем подзадачи решаются рекурсивно и объединяются, чтобы получить решение исходной задачи.

Подход «разделяй и властвуй» включает в себя следующие шаги на каждом уровне —

• Разделить — исходная проблема делится на подзадачи.

• Завоевать — Подзадачи решаются рекурсивно.

• Объединить — Решения подзадач объединяются, чтобы получить решение исходной проблемы.

Разделить — исходная проблема делится на подзадачи.

Завоевать — Подзадачи решаются рекурсивно.

Объединить — Решения подзадач объединяются, чтобы получить решение исходной проблемы.

Бинарный поиск является примером алгоритма разделяй и властвуй.

ПСЕВДОКОД

Binarysearch(a, b, low, high)

if low < high then
   return NOT FOUND
else
   mid ← (low+high) / 2
   if b = key(mid) then
      return key(mid)
   else if b < key(mid) then
      return BinarySearch(a, b, low, mid−1)
   else
   
      return BinarySearch(a, b, mid+1, high)

Поиск в глубину

Поиск в глубину (или DFS) — это алгоритм поиска в дереве или структуре данных неориентированного графа. Здесь концепция состоит в том, чтобы начать с начального узла, известного как корень, и пройти как можно дальше в той же ветви. Если мы получим узел без узла-преемника, мы вернемся и продолжим работу с вершиной, которую еще предстоит посетить.

Этапы поиска в глубину

• Рассмотрим узел (root), который ранее не посещался, и отметьте его как посещенный.

• Посетите первый соседний узел-преемник и отметьте его как посещенный.

• Если все последующие узлы рассматриваемого узла уже посещены или у него больше нет преемного узла, вернитесь к его родительскому узлу.

Рассмотрим узел (root), который ранее не посещался, и отметьте его как посещенный.

Посетите первый соседний узел-преемник и отметьте его как посещенный.

Если все последующие узлы рассматриваемого узла уже посещены или у него больше нет преемного узла, вернитесь к его родительскому узлу.

ПСЕВДОКОД

Пусть v будет вершина, с которой начинается поиск в графе G.

DFS(G,v)

   Stack S := {};
	
   for each vertex u, set visited[u] := false;
   push S, v;
   while (S is not empty) do
     u := pop S;
	  
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbour w of u
            push S, w;
      end if
		
   end while
   
END DFS()

Поиск в ширину

Поиск в ширину (или BFS) — это алгоритм поиска в дереве или структуре данных неориентированного графа. Здесь мы начинаем с узла, а затем посещаем все смежные узлы на одном уровне, а затем переходим на соседний узел-преемник на следующем уровне. Это также называется поиском по уровням .

Шаги поиска в ширину

• Начните с корневого узла, отметьте его как посещенный.
• Поскольку корневой узел не имеет узла на том же уровне, перейдите на следующий уровень.
• Посетите все соседние узлы и отметьте их как посещенные.
• Перейти на следующий уровень и посетить все не посещенные смежные узлы.
• Продолжайте этот процесс, пока все узлы не будут посещены.

ПСЕВДОКОД

Пусть v будет вершина, с которой начинается поиск в графе G.

BFS(G,v)

   Queue Q := {};
	
   for each vertex u, set visited[u] := false;
   insert Q, v;
   while (Q is not empty) do
      u := delete Q;
		
      if (not visited[u]) then
         visited[u] := true;
         for each unvisited neighbor w of u
            insert Q, w;
      end if
		
   end while
   
END BFS()

Best-First Search

Best-First Search — это алгоритм, который пересекает график, чтобы достичь цели по кратчайшему пути. В отличие от BFS и DFS, Best-First Search следует функции оценки, чтобы определить, какой узел является наиболее подходящим для прохождения следующего.

Шаги поиска Best-First

• Начните с корневого узла, отметьте его как посещенный.
• Найдите следующий соответствующий узел и отметьте его как посещенный.
• Перейдите на следующий уровень и найдите соответствующий узел и отметьте его как посещенный.
• Продолжайте этот процесс, пока цель не будет достигнута.

ПСЕВДОКОД

BFS( m )

   Insert( m.StartNode )
   Until PriorityQueue is empty
      c ← PriorityQueue.DeleteMin
      If c is the goal
      Exit
   Else
   
      Foreach neighbor n of c
         If n "Unvisited"
            Mark n "Visited"
            Insert( n )
      Mark c "Examined"
      
End procedure

Графовый алгоритм

Граф — это абстрактная нотация, используемая для представления связи между парами объектов. Граф состоит из —

• Вершины — взаимосвязанные объекты в графе называются вершинами. Вершины также известны как узлы .

• Края. Края — это ссылки, соединяющие вершины.

Вершины — взаимосвязанные объекты в графе называются вершинами. Вершины также известны как узлы .

Края. Края — это ссылки, соединяющие вершины.

Есть два типа графиков —

• Направленный граф — В ориентированном графе ребра имеют направление, то есть ребра переходят из одной вершины в другую.

• Ненаправленный граф. В неориентированном графе ребра не имеют направления.

Направленный граф — В ориентированном графе ребра имеют направление, то есть ребра переходят из одной вершины в другую.

Ненаправленный граф. В неориентированном графе ребра не имеют направления.

Раскраска графика

Раскраска графа — это метод назначения цветов вершинам графа, чтобы не было двух смежных вершин одинакового цвета. Некоторые проблемы раскраски графа —

• Раскраска вершин — способ раскраски вершин графа, чтобы никакие две смежные вершины не имели одинаковый цвет.

• Раскраска краев — это метод назначения цвета каждому ребру, чтобы два соседних ребра не имели одинаковый цвет.

• Раскраска граней — назначает цвет каждой грани или области плоского графа, чтобы никакие две грани с общей границей не имели одинакового цвета.

Раскраска вершин — способ раскраски вершин графа, чтобы никакие две смежные вершины не имели одинаковый цвет.

Раскраска краев — это метод назначения цвета каждому ребру, чтобы два соседних ребра не имели одинаковый цвет.

Раскраска граней — назначает цвет каждой грани или области плоского графа, чтобы никакие две грани с общей границей не имели одинакового цвета.

Хроматическое число

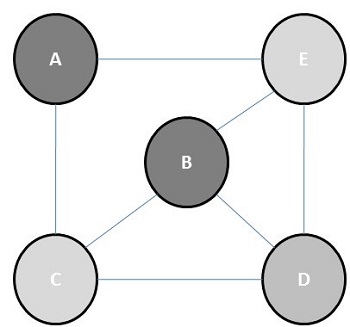
Хроматическое число — это минимальное количество цветов, необходимое для окраски графика. Например, хроматическое число следующего графика — 3.

Концепция раскраски графиков применяется при составлении расписаний, присвоении подвижной радиочастоты, Suduku, распределении регистров и раскраске карт.

Шаги для раскраски графа

• Установите начальное значение каждого процессора в n-мерном массиве в 1.

• Теперь, чтобы назначить конкретный цвет вершине, определите, назначен ли этот цвет соседним вершинам или нет.

• Если процессор обнаруживает тот же цвет в смежных вершинах, он устанавливает свое значение в массиве в 0.

• После n ² сравнений, если какой-либо элемент массива равен 1, то это допустимая раскраска.

Установите начальное значение каждого процессора в n-мерном массиве в 1.

Теперь, чтобы назначить конкретный цвет вершине, определите, назначен ли этот цвет соседним вершинам или нет.

Если процессор обнаруживает тот же цвет в смежных вершинах, он устанавливает свое значение в массиве в 0.

После n ² сравнений, если какой-либо элемент массива равен 1, то это допустимая раскраска.

Псевдокод для раскраски графа

begin

   create the processors P(i 0 ,i 1 ,...i n-1 ) where 0_i v < m, 0 _ v < n
   status[i0,..i n-1 ] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if a j,k =1 and i j =i k then
            status[i 0 ,..i n-1 ] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Минимальное остовное дерево

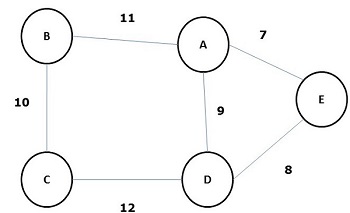
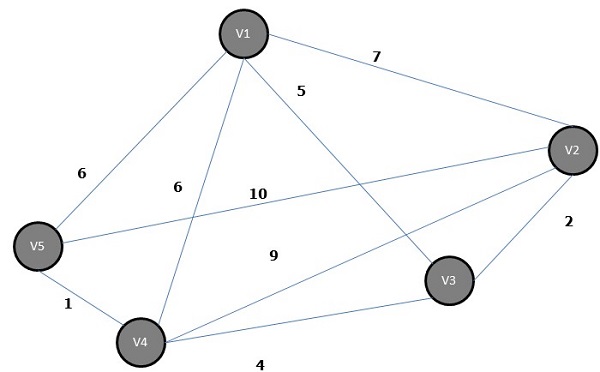
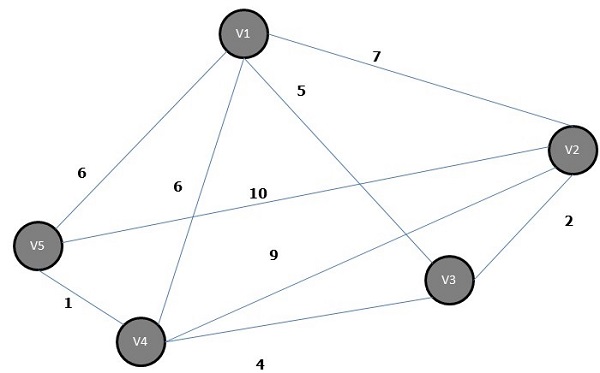
Остовное дерево, у которого сумма веса (или длины) всех его ребер меньше, чем у всех других возможных остовных деревьев графа G, называется минимальным остовным деревом или остовным деревом с минимальной стоимостью . На следующем рисунке показан взвешенный связный график.

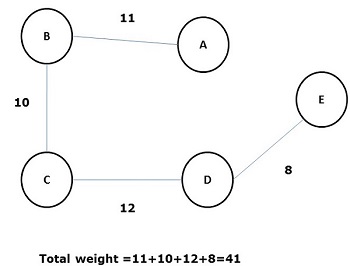
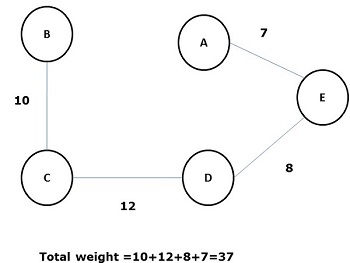
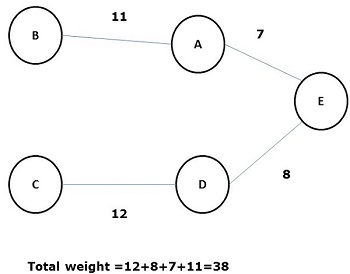
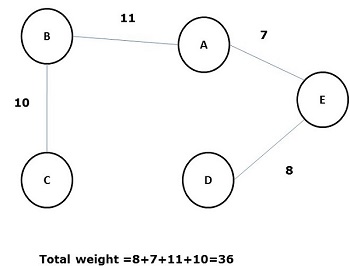
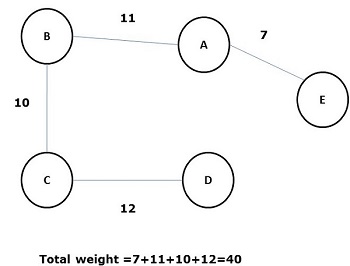
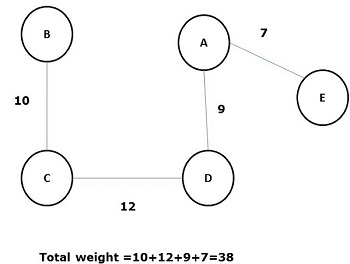
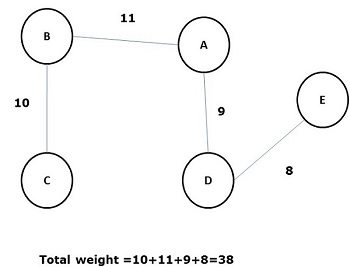
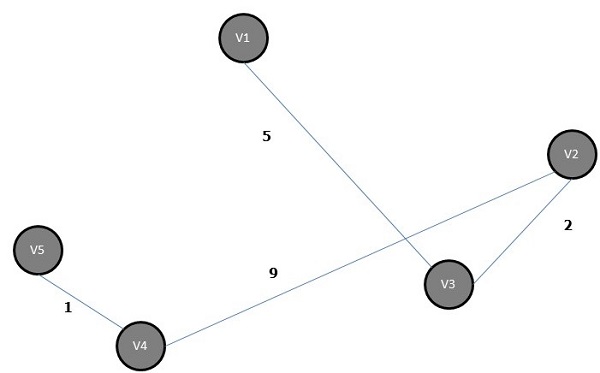
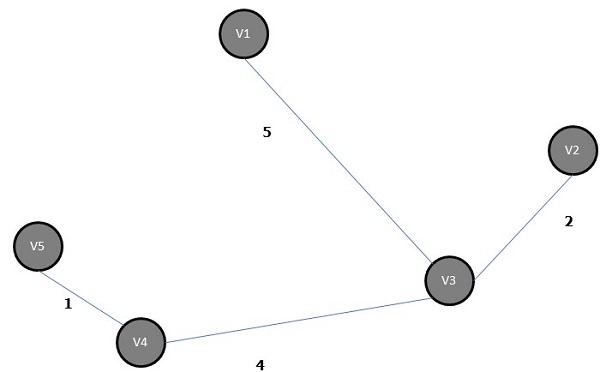
Некоторые возможные остовные деревья приведенного выше графика показаны ниже —

Среди всех вышеупомянутых остовных деревьев цифра (d) является минимальным остовным деревом. Концепция связующего дерева с минимальной стоимостью применяется в задачах коммивояжера, проектировании электронных схем, проектировании эффективных сетей и разработке эффективных алгоритмов маршрутизации.

Для реализации минимального связующего по стоимости дерева используются следующие два метода:

• Алгоритм Прима
• Алгоритм Крускала

Алгоритм Прима

Алгоритм Прима является жадным алгоритмом, который помогает нам найти минимальное остовное дерево для взвешенного неориентированного графа. Сначала он выбирает вершину и находит ребро с наименьшим весом, падающим на эту вершину.

Шаги алгоритма Прима

• Выберите любую вершину, скажем, v ₁ графа G.

• Выберите ребро, скажем, e ₁ из G так, что e ₁ = v ₁ v ₂ и v ₁ ≠ v _2, а e ₁ имеет минимальный вес среди ребер, падающих на v ₁ в графе G.

• Теперь, следуя шагу 2, выберите минимальное взвешенное ребро инцидента на v ₂ .

• Продолжайте до тех пор, пока не будут выбраны n – 1 ребра. Здесь n — количество вершин.

Выберите любую вершину, скажем, v ₁ графа G.

Выберите ребро, скажем, e ₁ из G так, что e ₁ = v ₁ v ₂ и v ₁ ≠ v _2, а e ₁ имеет минимальный вес среди ребер, падающих на v ₁ в графе G.

Теперь, следуя шагу 2, выберите минимальное взвешенное ребро инцидента на v ₂ .

Продолжайте до тех пор, пока не будут выбраны n – 1 ребра. Здесь n — количество вершин.

Минимальное остовное дерево —

Алгоритм Крускала

Алгоритм Крускала является жадным алгоритмом, который помогает нам найти минимальное связующее дерево для связанного взвешенного графа, добавляя дуги увеличивающейся стоимости на каждом шаге. Это алгоритм минимального связующего дерева, который находит ребро с наименьшим возможным весом, который соединяет любые два дерева в лесу.

Шаги алгоритма Крускала

• Выберите ребро минимального веса; скажем, е ₁ графа G и е ₁ не является петлей.

• Выберите следующий минимальный взвешенный край, связанный с e ₁ .

• Продолжайте до тех пор, пока не будут выбраны n – 1 ребра. Здесь n — количество вершин.

Выберите ребро минимального веса; скажем, е ₁ графа G и е ₁ не является петлей.

Выберите следующий минимальный взвешенный край, связанный с e ₁ .

Продолжайте до тех пор, пока не будут выбраны n – 1 ребра. Здесь n — количество вершин.

Минимальное остовное дерево приведенного выше графика —

Алгоритм кратчайшего пути

Алгоритм кратчайшего пути — это метод нахождения пути с наименьшей стоимостью от исходного узла (S) к узлу назначения (D). Здесь мы обсудим алгоритм Мура, также известный как алгоритм поиска в ширину.

Назовите исходную вершину S и назовите ее i и установите i = 0 .

Найдите все немаркированные вершины, смежные с вершиной, помеченной i . Если вершины S не связаны с вершиной, то вершина D не связана с S. Если есть вершины, связанные с S, обозначьте их i + 1 .

Если D помечен, то перейдите к шагу 4, иначе перейдите к шагу 2, чтобы увеличить i = i + 1.

Остановитесь после того, как длина кратчайшего пути найдена.